
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интервальные оценки параметров регрессионной модели
|
|
Если уравнение регрессии значимо => можно определять с надёжностью γ интервальные оценки параметров регрессионной модели.
а) Доверительный интервал для коэффициента регрессии β 0 с надёжностью γ:
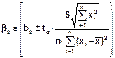
tα определяется по таблице распределения Стьюдента для α =1- γ и числа степеней свободы ν =n-2
б) Доверительный интервал для коэффициента регрессии β 1 с надёжностью γ:
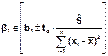
При n→ ∞ (n> 30) t определяется по таблице функции Лапласа для γ =Φ (t)
Ŝ – оценка остаточного среднеквадратического отклонения
7. Построение доверительного интервала для условного математического ожидания и доверительного интервала в точке предсказания x=xn+1
Доверительный интервал для условного математического ожидания при x=x0 с надёж. γ:
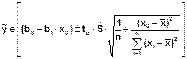
tα определяется по таб.2 распределения Стьюдента для α =1- γ и числа степеней свободы ν =n-2
При n→ ∞ (n> 30) t определяется по таблице функции Лапласа для γ =Φ (t)
Ŝ – оценка остаточного среднеквадратического отклонения
Доверительный интервал для интервала предсказания в точке x=xn+1 с надёж. γ:
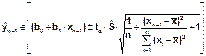
tα определяется по таб.2 распределения Стьюдента для α =1- γ и числа степеней свободы ν =n-2
При n→ ∞ (n> 30) t определяется по таблице функции Лапласа для γ =Φ (t)
Ŝ – оценка остаточного среднеквадратического отклонения