
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка значимости уравнения регрессии. Разложение дисперсий.
|
|
После того, как регрессионная модель построена, то есть найдены ее параметры, необходимо проверить ее адекватность исходным данным, а также полученную точность.
При соблюдении всех предпосылок регрессионного анализа можно проверить значимость уравнения регрессии, для чего следует проверить нулевую гипотезу
H0 : β 1=0
В основе проверки гипотезы H0 : β 1=0лежит идея дисперсионного анализа, состоящая в разложении дисперсии на составляющие.
В регрессионном анализе общая сумма квадратов отклонений зависимой переменной Qобщразлагается на
• сумму квадратов QR отклонений, обусловленных регрессией, которая характеризует воздействие объясняющей переменной,
• сумму квадратов Qост отклонений относительно плоскости регрессии, характеризующую воздействие неучтенных в модели или случайных факторов.
Qобщ=QR + Qост
где
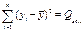
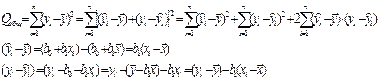
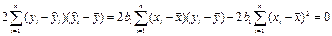
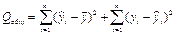
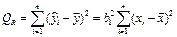
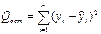
Для проверки значимости уравнения регрессии т.е. гипотезы H0: β 1=0
Используется F-критерий, основанный на статистике:
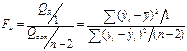
По таб.4 F-распределения Фишера-Снедекора находится Fкр (α; ν 1=1; ν 2=n-2).
Если Fн > Fкр, то гипотеза H0 отвергается с вероятностью ошибки и уравнение регрессии считается значимым.