Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случайные величины и их характеристики
|
|
§ Случайной величиной называют величину, которая в результате испытания примет одно возможное значение, заранее не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
§ Во многих случаях исходы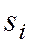 
случайного процесса – некоторые числа 
.
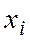В этом случае говорят о дискретной случайной величине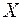 
, могущей принимать значения 
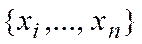с вероятностями соответственно 
.
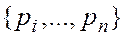§ Задание для каждого значения дискретной случайной величины 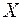вероятности, с которой это значение принимается, называется рядом распределения: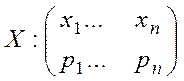 
§ Функцией распределения (или законом распределения) дискретной случайной величины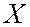 
называют вероятность 
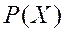того, что случайная величина примет значение, меньшее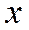 
§ Математическим ожиданием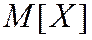 
или 
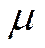дискретной случайной величины 
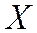называют ее среднее значение: 
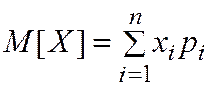(дает представление о «положении» случайной величины)
§ Центральным моментом порядка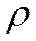 
дискретной случайной величины 
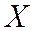называют математическое ожидание 
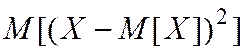случайной величины 
.
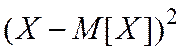§ Центральным моментом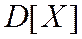 
порядка 2 называют дисперсией: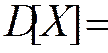 
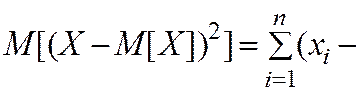
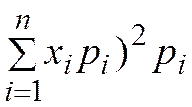
§ Средним квадратичным отклонением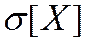 
дискретной случайной величины 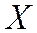называется 
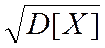(дает представление о «разбросанности» случайной величины)
§ Если случайная величина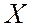 
принимает бесконечно много значений из некоторого множества действительных чисел, то ее функция распределения – это вероятность 
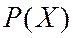того, что случайная величина примет значение, меньшее 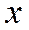. Если эта функция непрерывна, то случайная величина 
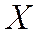называется непрерывной
§ Вероятность любого отдельного значения непрерывной случайной величины равна 0, поэтому имеет смысл говорить о вероятности того, что ее значение принадлежит некоторому множеству. Так, вероятность того, что значение 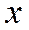случайной величины 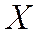принадлежит множеству 
, равна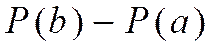 
.
§ Если 
функция распределения непрерывной случайной величины 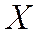является дифференцируемой, то удобно исследовать ее плотность распределения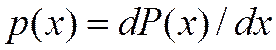 
§ Для непрерывной случайной величины 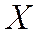, обладающей плотностью распределения, мат.ожидание и дисперсия: 