Экспериментальное определение числовых характеристик случайных величин

§ Пусть произведено 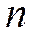опытов, в результате получено множество 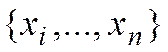значений случайной величины .

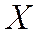§ Оценка математического ожидания :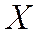

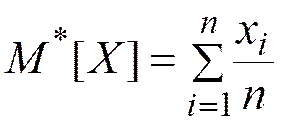(1)

§ Оценка дисперсии:

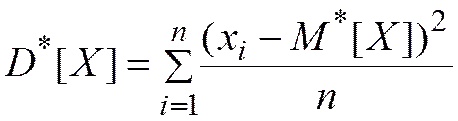(2)

§ Пусть 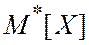, 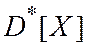- случайные величины, определенные по (1) и (2).

Тогда 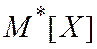= , т.е. экспериментальная оценка (1) – несмещенная,

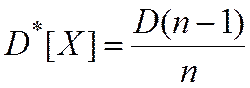, т.е. экспериментальная оценка (2) – смещенная.

§ Смещенность оценки (2) означает: если повторять много раз серию из 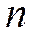опытов, получая каждый раз экспериментальные значения случайной величины 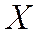и вычислять каждый раз значение 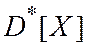, то оно будет колебаться не вокруг истинного значения дисперсии 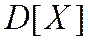, а вокруг значения 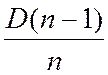, т.е. несмещенная оценка дисперсии равна: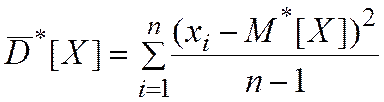

§ Задача оценки и надежности вычисления числовых характеристик случайной величины :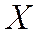

1. пусть по экспериментальным наблюдениям случайной величины вычислена оценка 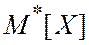ее математического ожидания.

2. пусть 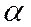- вероятность того, что величина 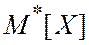отклонится от истинного математического ожидания не более, чем на .

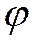3. 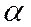- доверительная вероятность, характеризует точность полученного результата, интервал 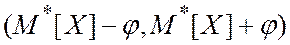- доверительный, характеризует надежность полученного результата, на практике обычно используется 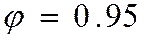, реже 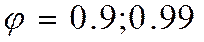, редко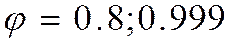

4. задав 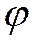, можно по имеющимся экспериментальным результатам оценить вероятность попадания вычисленного значения 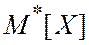в доверительный интервал