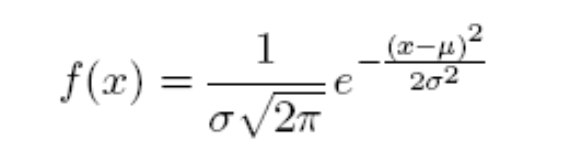Законы распределения случайных величин

· Дискретные случайные величины:

1) дискретное равномерное распределение: (параметр 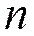) 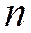равновероятных событий,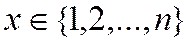

2) биномиальное: (параметры 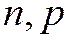) число успехов в 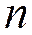независимых испытаниях Бернулли, вероятность успеха каждого равна 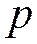, 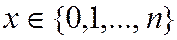. Варианты применения: количество «поврежденных» товаров в партии размером 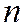; число объектов в группе случайного размера; число товаров, затребованных из запасов.

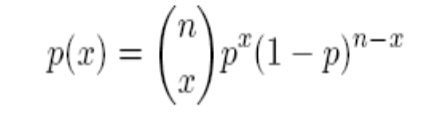
3) геометрическое: (параметр 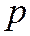) число испытаний до первого успеха в последовательности независимых испытаний Бернулли,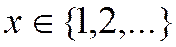

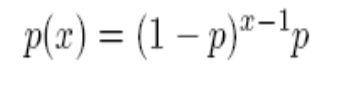
4) Пуассона: (параметр 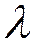), 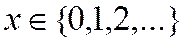. Варианты применения: число событий, возникающих в интервале времени, когда события происходят с постоянной интенсивностью .

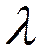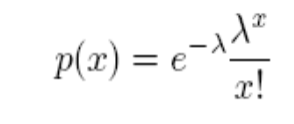
Многие реальные случайные величины распределены по закону Пуассона

· Непрерывные случайные величины:

1) равномерное распределение: (параметры 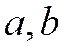) «первая» модель величины, которая случайно изменяется между 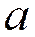и 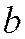, но о которой больше ничего неизвестно,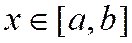

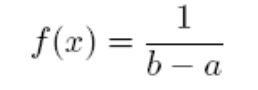
2) экспоненциальное распределение: (масштабный параметр 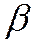), Варианты применения: интервал времени между поступлениями требований в систему, проходящими с постоянной интенсивностью; время безотказной работы устройства

Плотность распределения :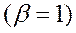

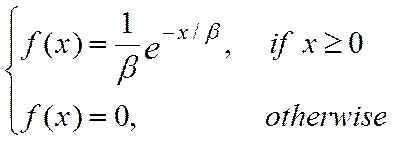
4) нормальное распределение (функция Лапласа): (параметры 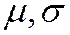), 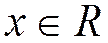Варианты применения: ошибки различного рода, например, точка попадания снаряда; величины, представляющие собой сумму большого количества других величин (на основании центральной предельной теоремы)