Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые характеристики дискретных случайных величин
|
|
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.
Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго.
Математическое ожидание дискретной
случайной величины
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть случайная величина X может принимать только значения xl x2,..., хп, вероятности которых соответственноравны p1, p2, p3, … рп . Тогда математическое ожидание М (X) случайной величины X определяется равенством
М (X) = xlpl + х2р2 +... + хпрп.
Пример 1. Найти математическое ожидание случайной величины X, зная закон ее распределения:
| X | |||
| р | 0, 1 | 0, 6 | 0, 3 |
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:
М (Х) = 3 × 0, 1+5 × 0, 6 + 2 × 0, 3 = 3, 9.
Дисперсия
Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения. Рассмотрим, например, дискретные случайные величины X и У, заданные следующими законами распределения:
| X | - 0, 01 | 0, 01 | У | -100 | ||
| р | 0, 5 | 0, 5 | р | 0, 5 | 0, 5 |
Найдем математические ожидания этих величин:
М(Х) =-0, 01× 0, 5 + 0, 01 × 0, 5 = 0,
М (У) = -100 × 0, 5+100 × 0, 5 = 0.
Здесь математические ожидания обеих величин одинаковы, а возможные значения различны, причем X имеет возможные значения, близкие к математическому ожиданию, а У - далекие от своего математического ожидания. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.
По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
Прежде чем перейти к определению и свойствам дисперсии, введем понятие отклонения случайной величины от ее математического ожидания.
Отклонением называют разность между случайной величиной и ее математическим ожиданием: Х – М(Х)
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. М [X— М (X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие -отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Д(Х) = М [X— М (X)] 2
Из этой формулы следует, для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.
Пример:
Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
| X | |||
| р | 0, 3 | 0, 5 | 0, 2 |
Найдем математическое ожидание:
М(Х) = 1 × 0, 3 + 2 × 0, 5 + 5 × 0, 2 =2, 3
Найдем все возможные значения квадрата отклонения случайной величины от математического ожидания:
[ х 1— М (X)] 2 = (1— 2, 3) 2= 1, 69
[ х2 — М (X)] 2 = (2— 2, 3) 2=0, 09
[ х 3— М (X)] 2 = (5— 2, 3) 2= 7, 29.
Напишем закон распределения квадрата отклонения:
| [ х 1— М (X)] 2 | 1, 69 | 0, 09 | 7, 29 |
| р | 0, 3 | 0, 5 | 0, 2 |
По определению дисперсии
Д(Х) = 1, 69 × 0, 3 + 0, 09 × 0, 5 + 7, 29 × 0, 2 = 2, 01
Данный способ вычисления дисперсии достаточно громоздкий. В математике доказана теорема, которая позволяет вычисления дисперсии более простым способом.
Теорема: Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
Д(Х) = М(Х2) —[М (X)] 2
Эта теорема позволяет искать значение дисперсии другим способом.
Пример: Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
| X | |||
| р | 0, 3 | 0, 5 | 0, 2 |
Найдем математическое ожидание:
М(Х) = 1 × 0, 3 + 2 × 0, 5 + 5 × 0, 2 =2, 3
Напишем закон распределения случайной величины Х2:
| X 2 | 12 | 22 | 52 |
| р | 0, 3 | 0, 5 | 0, 2 |
Найдем математическое ожидание М(Х 2):
М(Х 2) = 1 × 0, 3 + 4 × 0, 5 + 25 × 0, 2 = 0, 3+2+5=7, 3
Тогда дисперсия равна
Д(Х) = М(Х2) —[М (X)] 2= 7, 3 – (2, 3)2 = 2, 01.
Задача. Сравнить дисперсии случайных величин, заданных законами распределения:
| X | - 1 | У | -1 | |||||||
| р | 0, 48 | 0, 01 | 0, 09 | 0, 42 | р | 0, 19 | 0, 51 | 0, 23 | 0, 05 |
Посчитав математическое ожидание каждой величины, получим М(Х) = М(У) = 0, 97
Посчитаем дисперсию каждой величины:
| X2 | -1 | У2 | -1 | |||||||
| р | 0, 48 | 0, 01 | 0, 09 | 0, 42 | р | 0, 19 | 0, 51 | 0, 23 | 0, 05 |
М(Х2) = -1 × 0, 48 + 1 × 0, 01 + 4 × 0, 09 + 9 × 0, 42 = 3, 67
Д(Х) = 3, 67 – 0, 972 = 2, 73
М(У2) = -1 × 0, 19 + 1 × 0, 51 + 4 × 0, 23 + 9 × 0, 05 = 2, 07
Д(У) = 2, 07 –0, 972 = 1, 69
Итак, возможные значения математического ожидания двух распределений одинаковы, а дисперсии различны, причем Д(Х) > Д(У).
Случайная величина и ее математическое ожидание имеют одну размерность, а дисперсия имеет размерность квадрата случайной величины. Этого недостатка можно избежать, если ввести еще одну характеристику – среднее квадратичное отклонение, значение которого определить как квадратный корень из дисперсии.
Среднее квадратичное отклонение s(Х) = 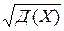 .
.
В рассмотренной выше задача s(Х) = 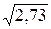 = 1, 65, а s(У) =
= 1, 65, а s(У) = 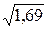 = 1, 3.
= 1, 3.
Математическое ожидание, дисперсия, среднее квадратичное отклонение и другие числа позволяют в сжатой форме описать наиболее общие черты распределения, их называют числовыми характеристиками случайной величины.
Следует заметить: сама величина Х – случайная, а ее числовые характеристики являются величинами неслучайными, а постоянными. Поэтому их часто называют параметрами распределения случайной величины. При решении практических задач приходится чаще оперировать параметрами распределения, оставляя в стороне законы распределения.
Функция распределения случайной величины.
До сих пор в качестве полного описания дискретной случайной величины мы рассматривали ее закон распределения. Однако такое описание случайной величины Х не является единственным и более того, он не универсально. Этот способ не подходит для описания непрерывной случайной величины.
Для описания поведения случайной величины Х возможен и другой подход. Можно рассматривать не все вероятности Х = х для разных х, как это происходит в ряде распределения, вероятности события Х < х, где х – текущая переменная. Тогда вероятность Р(Х < х) зависит от х, то есть является функцией от х. Обозначим эту функцию F(x).
Определение. Функцией распределения случайной величины X называется функция F(x), задающая вероятность того, что случайная величина X принимает значение, меньшее х.
F(x) = P(X< x) (1)
Иногда функцию F(x) называют интегральной функцией распределения. Такую функцию можно построить как для дисретной, так и для непрерывной величины.
Построим теперь функцию F(x) распределения случайной величины, ряд распределения которой представлен в таблице.
| X | ||||
| р | 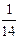
| 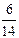
| 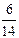
| 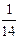
|
По определению F(x) = P(X< x) = 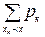 . Тогда
. Тогда
А) при х £ 1 F(x) = P(X< 1)= 0 (в том числе и для х = 1, так как F(1) = P(X< 1) =0)
Б) при 1 < х £ 2 F(x) = P(X=1) = 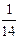
В) при 2 < х £ 3 F(x) = P(X=1) + Р(Х=2) = 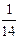 +
+ 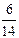 =
= 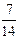 =
= 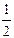
Г) при 3 < х £ 4 F(x) = P(X=1) + Р(Х=2) + Р(Х=3) = 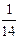 +
+ 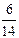 +
+ 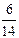 =
= 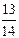
Д) при х > 4 F(x) = P(X=1) + Р(Х=2)+ Р(Х=3) + Р(Х=4) = 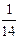 +
+ 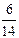 +
+ 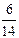 +
+ 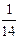 = 1
= 1
Следовательно:  F(x) =
F(x) = 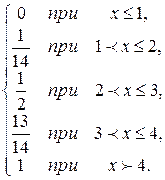 .
.
По заданной функции можно построить ее график.
Полученная нами функция распределения имеет следующий график:
 |
Для дискретной случайной величины график функции распределения представляет собой разрывную ступенчатую линию. Когда переменная х проходит через какое-нибудь из возможных значений случайной величины, значение функции распределения меняется скачкообразно, т. е. функция имеет скачок в тех точках, в которых случайная величина принимает конкретное значение согласно ряду распределения, причем величина скачка равна вероятности этого значения. Сумма величин всех скачков функции распределения равна 1. В интервалах между значениями случайной величины функция F(x) постоянна. Отметим, что по функции распределения дискретной случайной величины можно легко восстановить ее ряд распределения.
Функция распределения случайной величины обладает следующими свойствами:
1) Область значений функции: [0; 1].
2) Функция распределении яслучайной величины есть неубывающая функция.
3) Вероятность попадания случайной величины в интервал [х1; х2) равна приращению функции на этом интервале: Р(х1≤ Х< х2) = F(х2) - F(х1)
Предположим, что график функции F(x) распределения описывает число стандартных деталей среди четырех отобранных. Она имеет четыре скачка по числу принимаемых случайной величиной X значений. По мере возрастания числа возможных значений случайной величины с одновременным уменьшением величины интервалов между ними число скачков становится больше, а сами скачки — меньше, вследствие чего ступенчатая кривая становится более плавной. В этом случае дискретная случайная величина постепенно приближается к непрерывной, а ее функция распределения — к непрерывной функции. Ниже представлен график непрерывной функции (в данном случае функции нормального распределения).