
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Плотность распределения вероятностей. Функция распределения вероятностей непрерывной случайной величины дает полную вероятностную характеристику ее поведения
|
|
Функция распределения вероятностей непрерывной случайной величины дает полную вероятностную характеристику ее поведения. Однако задание непрерывной случайной величины с помощью функции распределения не является единственным. Ее можно задать с помощью другой функции, которая называется дифференциальной функцией распределения или плотностью распределения вероятностей. В некотором смысле эта функция «более удобная», чем интегральная функция F(x). Используя функцию F(x), трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси. Решить эту задачу позволяет плотность распределения вероятностей.
Определение. Плотностью распределения вероятностей непрерывной случайной величины называется первая производная интегральной функции распределения F(x).
f(x)= F'(x)
График плотности распределения вероятностей f(x) называется кривой распределения. Ниже представлен график плотности нормального распределения.

Пример 2. Непрерывная случайная величина задана функцией распределения вероятностей
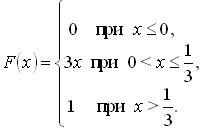
Найти функцию плотности распределения вероятности.
Решение: Плотность распределения вероятностей f(x) непрерывной случайной величины вычисляется по формуле: f(x) = F’(x). Тогда (3x)’=3, (1)’ = 0 и

Пример 3. Непрерывная случайная величина задана функцией распределения вероятностей
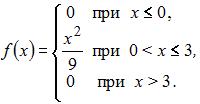
Чему равна вероятность 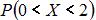 ?
?
Решение:
Воспользуемся формулой: Р(х1 < Х < х2) = 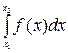 = F(x2) – F(x1). Тогда
= F(x2) – F(x1). Тогда
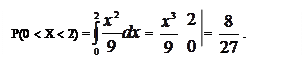 |