Теоретичні відомості. Автомат є математичною моделлю деякого пристрою чи системи дискретної дії

Автомат є математичною моделлю деякого пристрою чи системи дискретної дії. Така система деяку кількість вхідних та вихідних каналів і множину внутрішніх станів. Від вхідного сигналу змінюється стан системи та вихідний сигнал. Найбільш часто розглядаються скінчені автомати, в яких ці три множини скінчені.

Автомат розглядається як п’ятірка

{A, X, Y, d, l} (2.1)

де А – скінчена множина внутрішніх станів, Х – скінчена множина вхідних сигналів, Y – скінчена множина вихідних сигналів; d: А´ Х®А – однозначна функція переходів (із стану в стан), l: А´ Х® Y – однозначна функція виходів.

При невеликій кількості станів автомат часто описують за допомогою діаграми станів автомату (графу станів). Це напрямлений граф, вершини якого відповідають станам, а ребра сигналам, що з’єднують стани; назва ребра є назвою (кодом) сигналу; воно напрямлене від стану, в якому система знаходилася, до стану, в який система перейде під впливом даного сигналу.

На рис. 2.1 зображено автомат, який виконує додавання в двійковій системі числення.

Q₀ – стан, в якому немає переносів.

Q₁ – стан, в якому виконано додавання одиниці, яка попередньо запам’яталася.

Q₂ – стан, в якому виконано два переносу одночасно.

Q₃ – стан, в якому запам’яталася одиниця для переносу в старший розрад.

Q₀ та Q₁ є кінцевими станами, а Q₂ та Q₃ – проміжними.

Якщо станів багато, то для опису автомату використовують таблиці. Елемент таблиці А_ij містить рядок x: y, де х – код сигналу, що переводить систему зі стану I в стан j, а у – вихідний сигнал.

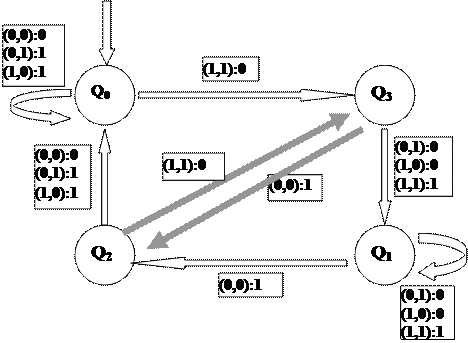
Рис. 2.1 Приклад. Суматор двійкових чисел

Досить широко зустрічаються такі різновиди автомату, у яких перехід із одного стану в інший виконується не детерміновано, а з певною ймовірністю. Такі автомати називаються стохастичними, тому що з зміною стану змінюється розподіл ймовірностей переходів.

Стохастичний автомат — це такий процес або об’єкт, який має обмежену кількість станів, в яких він може знаходитись і задані ймовірності переходів з кожного стану в будь-який інший.

Теоретичною базою стохастичного автомату є теорія марківських процесів. Не всі види марківських процесів є стохастичними автоматами. Марківськими називаються такі випадкові процеси в довільній системі для яких в будь який момент часу ймовірність переходу системи в інші стани не залежить від того, як система прийшла в даний стан, а залежить тільки від теперішнього стану системи.

Розрізняють наступні види марківських процесів:

· З дискретними станами та дискретним часом (ланцюг Маркова);

· З неперервними станами та дискретним часом (марківські послідовності);

· З дискретними станами та неперервним часом (неперервні ланцюги Маркова);

· З неперервним часом та неперервними станами.

Як стохастичний автомат розглядаються тільки процеси з дискретними станами. Стохастичним автоматом моделюється багато різноманітних процесів: процес загибелі та розмноження в біологічних системах, вибір покупцем товару в маркетингових дослідженнях тощо. В технічних задачах найбільш часто за допомогою стохастичного автомата моделюють технічний стан різних пристроїв. На рис. 2.2 показано приклад такої моделі, що описує літальний апарат (спрощено з [4]). Тут Г – стан готовності до польоту, КР – капітальний ремонт; С – списання; Р – ремонт; РР – регламентні роботи.

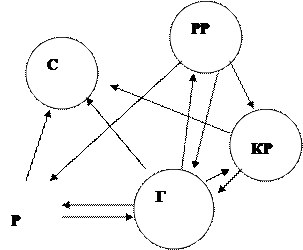
Рис. 2.2 Граф станів літального апарату