
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поглинаючі ланцюги
|
|
Канонічна форма матриці переходів
Для поглинаючих ланцюгів це така форма матриці, в якій рядки і колонки матриці переставлені таким чином, що поглинаючі стани займають перші рядки та колонки. Ця матриця має наступну структурну форму:
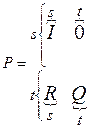 (2.8)
(2.8)
Вона складається як би з чотирьох матриць, де I – одинична, а 0 – нульова матриці.
Фундаментальна матриця ланцюга
. Фундаментальна матриця ланцюга визначається наступним чином
N=(I-Q)-1 (2.9)
Елементи матриці показують середню кількість попадань в відповідні стани (номер колонки), якщо рух починати зі стану, що відповідає номеру рядка
Інша необхідна інформація обчислюється з наступних формул
1. Дисперсія числа попадань процесу в деякий заданий стан при певному початковому стані: N2=N(2Ndiag–I)–N [1] sqr. (2.10). Елементи матриці показують дисперсію кількості попадань в відповідні стани (номер колонки), якщо рух починати зі стану, що відповідає номеру рядка.
2. Середнє значення та дисперсія числа попадань процесу в заданий нестійкий стан. t2=(2N–I)t-t2; (2.11)де t=Nx, а x – одиничний вектор.
3. Ймовірність того, що процес попаде в заданий поглинаючий стан (номер колонки), якщо він почне рух з заданого нестійкого стану (номер рядка) B=NR. (2.12)
Приклад
Процес описується наступною матрицею переходів:
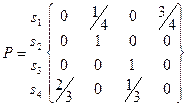
Після перестановок рядків та колонок отримаємо наступну канонічну форму матриці переходів:
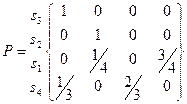
Зверніть увагу, що рядки тепер мають нові назви! Звідси
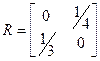
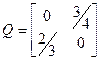 .
.
Тоді канонічна матриця ланцюга матиме наступний вигляд
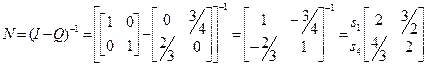
Після цього
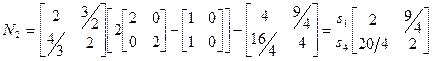
Таким чином, якщо почати рух зі стану s1, то середнє число попадань в стан s4 (до того, як система попаде в один з поглинаючих станів) буде 3/2, а в s1– 2. Дисперсія цих значень дорівнює відповідно 9/4 і 20/4.
Далі визначаємо
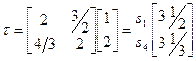
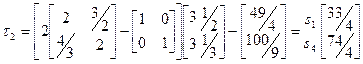
Тобто, середнє значення числа попадань процесу в стан s1 до поглинання 3, 5 при дисперсії цього значення 33/4.

Тобто, якщо процес почнеться зі стану s1, то він з однаковою ймовірністю закінчиться в s3, або s2, Якщо ж він почнеться з s4, то ймовірність завершитися в s3 дорівнює 2/3.
Література
1. Е.В. Бережная, В.И. Бережной Математические методы моделирования экономических систем –М.: Финансы и статистика, 2001. –368с.
2. Бусленко Н.П., Калашников В.В., Коваленко И.Н. Лекции по теории сложных систем. М.: Советское радио. –1973, –440с.
3. Вентцель Е.С. Теория вероятностей –М.: –Высшая школа, –1999. –576с.
4. Волков Л.И. Управление эксплуатацией летательных комплексов –М.: ВШ, 1981. –368с.
5. Енциклопедія кібернетики, у 2-х тт.., Т1.584с. Т2. 574с К.: УРЕ, 1973
6. Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику –М.: Изд-во “Иностранная литература”. –1963. –486с.
7. Креденцер Б.П. Прогнозирование надежности систем с временной избыточностью –К.: Наукова думка, –1978. –240с.
8. Д.Кук, Г. Бейз Компьютерная математика М.: Наука, 1990.–384с.
9. Феллер В. Введение в теорию вероятностей и её приложения: в 2-х тт.Т1: Мир, –1984. –528с.
10. Д. Тёрнер Вероятность, статистика и исследование операций –М.: Статистика, –1976. –431с.

| Результати пошуку ймовірностей ергодичного стану | ||||
| Стан | Q | W | R | |
| Ймовірність | 0, 333333 | 0, 533333 | 0, 133333 | |
| Кроків: | ||||
| Q | W | R | ||
| Ймовірність | 0, 355469 | 0, 524922 | 0, 119609 | |
| Q | 0, 5 | 0, 5 | |
| W | 0, 3125 | 0, 5 | 0, 1875 |
| R | 0, 75 | 0, 25 |