Класифікація ланцюгів.

1. Поглинаючі ланцюги Маркова. Це такі ланцюги, в яких стійкі стани є поглинаючими.

2. Ергодичні ланцюги. Це такий ланцюг, який складається з одного ергодичної множини. Розділяються на циклічні, в яких процес приходить в кожен стан через певні інтервали і регулярні – неперіодичні ергодичні ланцюги.

Наприклад, автомат описується наступною матрицею переходів:

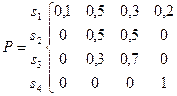(2.2)

Тут є дві групи ергодичних станів: в першу входять стани s₂ та s₃, а в другу – s₄. При цьому s₄ є поглинаючим станом.

Простий однорідний ланцюг Маркова визначається вектором ймовірностей станів у початковий момент

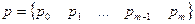(2.3)

і матрицею ймовірностей переходу.

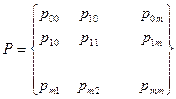(2.4)

При цьому для кожного рядка матриці виконується умова

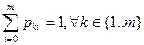(2.5)

Такий ланцюг має наступні властивості:

Простий – закон розподілу (рядок матриці) залежить тільки від стану, в якому система знаходиться.

Однорідний – якщо ймовірності переходу на певному інтервалі залежать тільки від довжини інтервалу, а не від точки відліку.

P(t_i)= P(t₀)Pⁱ(t) (2.6)

Ергодичний - з кожного стану можна попасти в будь-який інший.

Для ергодичного ланцюга існує граничний стан, в якому всі рядки матриці однакові.

Для визначення граничного стану розв’язується система рівнянь наступного виду (система рівнянь Колмогорова):

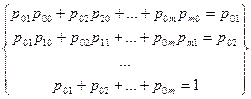(2.7)

При вивчення поведінки ланцюгів звичайно з`ясовуються наступні питання.

1. Ймовірність переходу зі стану i в стан j через n кроків.

2. Очікувана кількість попадань процесу в конкретний нестійкий стан.

3. Середнє значення (і дисперсія) числа кроків, які необхідно зробити процесу для переходу із одного конкретного стану в інший.

4. Ймовірність попасти із конкретного нестійкого стану в задану ергодичну підмножину станів.

5. Середнє число кроків (і дисперсія), котрі пройде процес перед тим, як попасти в ергодичну підмножину станів.