Средняя ошибка выборки

Случайная ошибка репрезентативности зависит от следующих фактов (при этом считается, что ошибок регистрации нет):

1. Чем больше численность выборки при прочих равных условиях, тем меньше величина ошибки выборки, т.е. ошибка выборки обратно пропорциональна ее численности.

2. Чем меньше варьирование признака, тем меньше ошибка выборки. Если признак совсем не варьирует, а, следовательно, величина дисперсии равна нулю, то ошибки выборки не будет, т.к. любая единица совокупности будет совершенно точно характеризовать всю совокупность по этому признаку. Таким образом, ошибка выборки прямо пропорциональна величине дисперсии.

В математической статистике доказывается, что величина средней ошибки случайной повторной выборки может быть определена по формуле

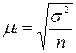(6.1)

Однако следует иметь в виду, что величина дисперсии в генеральной совокупности s ² нам не известна, т.к. наблюдение выборочное. Мы можем рассчитать лишь дисперсию в выборочной совокупности S². Соотношение между дисперсиями генеральной и выборочной совокупности выражается формулой:

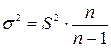(6.2)

Если n велико, следовательно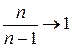

Таким образом, можно приблизительно считать, что выборочная дисперсия равна генеральной дисперсии.

s ² = S²

И формула средней ошибки повторной выборки (6.1.) примет вид:

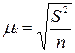(6.3)

Но здесь мы рассмотрели только ошибку выборки для средней величины интересующего признака. Существует также показатель доли единиц с интересующим признаком. Расчет ошибки этого показателя имеет свои особенности.

Дисперсия для показателя доли признака определяется по формуле:

S²=w(1-w) (6.4)

Тогда средняя ошибка повтора выборки для показателя доли признака будет равна:

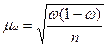(6.5)

Доказательство формул (6.3) и (6.5) исходит из схемы повторной выборки. Обычно же выборку организуют бесповторным способом. Т.к. при бесповторном отборе численность генеральной совокупности N в коде выборки сокращается, то в формулы ошибки выборки включают дополнительный множитель 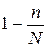, и формулы принимают вид:

(6.6)

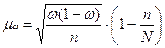(6.7)

Пример 1. Определим, на сколько отличаются выборочные и генеральные показатели по данным 10%-ной бесповторной выборки успеваемости студентов.

Расчет ошибки бесповторной выборки для средней величины:

n = 100 N = 1000

Найдем выборочную дисперсию по формуле:

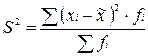
Здесь не известна величина 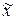, которую можно найти как обычную среднюю взвешенную величину:

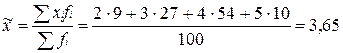
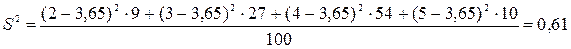
Таким образом,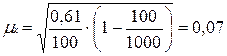

Т.е. можно сказать, что средний балл всех студентов () равен 3, 65±0, 07

Теперь рассчитаем долю студентов в генеральной совокупности, обучающихся на «4» и «5».

Найдем по выборке долю студентов, получивших оценки «4» и «5».

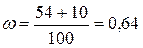(или 64%)

Расчет ошибки бесповторной выборки для доли производится по формуле:

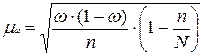
(или 4, 5%)

Таким образом, доля студентов, обучающихся на «4» и «5» по генеральной совокупности (P)составляет 0, 64±0, 045 (или 64%±4, 5%).