
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предельная ошибка выборки
|
|
То, что генеральная средняя и генеральная доля не выйдут за определенные пределы можно утверждать не с абсолютной достоверностью, а лишь с определенной степенью вероятности.
В математической статистике доказано, что генеральные характеристики отклоняются от выборочных на величину ошибки выборки (± m), лишь с вероятностью 0, 683. Применительно к выборочным исследованиям это понимается так, что значения пределов можно гарантировать лишь в 683 случаях из 1000. В остальных же 317 случаях значения этих пределов будут иными.
Вероятность суждения можно повысить, если расширить пределы отклонений, приняв в качестве меры среднюю ошибку выборки, увеличенную в t раз.
Т.е. с определенной степенью вероятности мы можем утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки D (дельта):
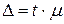 (6.8)
(6.8)
где t – коэффициент доверия (коэффициент кратности ошибки), определяемый в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного исследования.
На практике пользуются таблицами, где вычислены вероятности для различных значений t. Приведем некоторые из них.
| t | Вероятность | t | Вероятность |
| 0, 5 | 0, 383 | 2, 0 | 0, 954 |
| 1, 0 | 0, 683 | 2, 5 | 0, 988 |
| 1, 5 | 0, 866 | 3, 0 | 0, 997 |
Например, если в нашем примере мы хотим увеличить вероятность суждения до 0, 954, то мы берем t = 2 и таким образом изменяем пределы отклонений среднего балла всех студентов и доли студентов, обучающихся на «4» и «5».
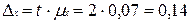
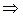
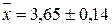
То есть, 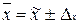 (6.9)
(6.9)
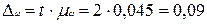
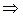
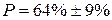 То есть,
То есть, 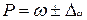 (6.10)
(6.10)