
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение численности выборки
|
|
При организации выборочного исследования следует иметь в виду, что размер ошибки выборки прежде всего зависит от численности выборочной совокупности. Из формулы (6.3) следует, что средняя ошибка выборки обратнопропорциональна 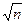 , т.е. при увеличении численности выборки, например в 4 раза, ее ошибки уменьшаются вдвое. Таким образом, увеличивая численность выборки можно довести ее ошибку до сколь угодно малых размеров. Повышение процента выборки ведет к увеличению объема исследовательской работы, затрат труда и материальных средств. Но если в выборку взять недостаточное количество образцов, то результаты исследования могут содержать большие погрешности. Путем несложного преобразования выведенных ранее формул ошибки выборки можно получить формулы для определения необходимой численности выборки.
, т.е. при увеличении численности выборки, например в 4 раза, ее ошибки уменьшаются вдвое. Таким образом, увеличивая численность выборки можно довести ее ошибку до сколь угодно малых размеров. Повышение процента выборки ведет к увеличению объема исследовательской работы, затрат труда и материальных средств. Но если в выборку взять недостаточное количество образцов, то результаты исследования могут содержать большие погрешности. Путем несложного преобразования выведенных ранее формул ошибки выборки можно получить формулы для определения необходимой численности выборки.
Для примера рассмотрим вывод формулы численности повторной выборки для средней величины признака.
Формула предельной ошибки повторной выборки для средней величины имеет вид:
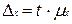 ,
, 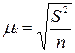
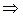
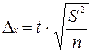
Выразим из последней формулы величину n (численность выборки). Для того, чтобы избавиться от знака корня, возведем всю формулу в квадрат и произведем дальнейшие математические преобразования:
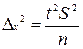
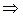
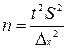 (6.11)
(6.11)
Ниже в таблице приведены остальные формулы численности выборки. Их вывод попробуйте сделать его самостоятельно.
| Метод отбора | Формулы численности выборки | |
| Для средней | Для доли | |
| Повторный | 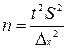 (6.11) (6.11)
| 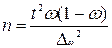 (6.13) (6.13)
|
| Бесповторный | 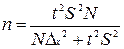 (6.12) (6.12)
| 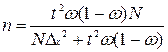 (6.14) (6.14)
|
При определении необходимой численности выборки по приведенным формулам возникает затруднение, т.к. S2 и w заранее не известны, а будут определены лишь после проведенного выборочного исследования.
Вместо фактического значения S2 и w подставляют приближенное значение, полученное из предыдущих исследований или на основе каких-либо пробных выборочных исследований.
Пример 2. Для исследования средней заработной платы 10000 рабочих завода необходимо провести выборочное исследование. Каков должен быть объем выборки, чтобы можно было бы утверждать, что ошибка выборки не превысит 1 рубль (с вероятностью 0, 997). Дисперсия заработной платы 150. Отбор бесповторный.
Решение: Формула численности бесповторной выборки для средней величины имеет вид (из таблицы):
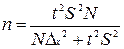
Нам известно: t = 3; 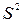 = 150; N = 10000;
= 150; N = 10000; 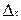 = 1
= 1
Таким образом 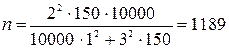 (11, 89%)
(11, 89%)