
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Педагогического эксперимента
|
|
Педагогические исследования в области физического воспитания и спорта связаны, прежде всего, с изучением учебно-тренировочного процесса и направлены на выявление эффективности той или иной методики обучения, тренировки и оздоровительной работы.
Для оценки результатов педагогического воздействия широко используются методы качественного и количественного анализов. В последние годы происходит интенсивный процесс внедрения количественных методов, основанных на использовании математического аппарата, практически во все отрасли науки. Не составляют исключения и педагогические. Однако следует отметить, что педагогические исследования имеют ряд особенностей, которые не позволяют применять эти методы по аналогии с тем, как это делается в естественных или технических науках. Незнание этих особенностей приводит к некорректному, формальному использованию математического аппарата, мешает сформулировать правильные выводы. Чтобы не допустить этого, необходимо иметь определенные знания и понимание студентами существа этих методов.
Примечание. Можно проводить сравнение отдельно по классам, по полу, занятий физической культурой и спортом. Это зависит от постановки цели и задач проводимого тестирования.
· Среднее арифметическое – M (среднее значение результатов показанных учащимися);
· Среднее квадратическое отклонение – σ (мера рассеяния результатов, показанных учащимися от более низких к более высоким, при этом самые низкие и самые высокие математически отбрасываются).
Примечание. Значение среднего арифметического не даёт полной информации о варьирующем признаке. Нетрудно представить себе два эмпирических распределения, у которых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки и записываются в виде М + σ.
· Ошибка среднего арифметического – m (отклонение оценок генеральных параметров, в частности среднего арифметического, от истинных значений этих параметров называются статистическими ошибками. В качестве оценки стандартного отклонения выборочного среднего используется величина называемая ошибкой среднего арифметического, которая показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего арифметического его выборочную оценку. Поэтому вычисление среднего арифметического часто указывается в виде М + m для более точной оценки среднего арифметического)
· Число степеней свободы для двух наборов - v
· t - критерий Стьюдента
· На основании t-критерия и v определяли степень достоверности Р (уровень значимости) полученных результатов используя таблицу.
Примечание. Р – экспериментальный уровень значимости. Точное значение обычно не указывают, а окончательные результаты приводят в следующем виде: 1) если вычисленное значение t не превосходит критического значения на уровне значимости α =0, 05, то различие считается статистически не значимым; 2) если вычисленное по выборке значение критерия превышает критические значения при α =0, 05 (5%), α =0, 01 (1%) или α =0, 001 (0, 1%), то записывают Р< 0, 05, Р< 0, 01 или Р< 0, 005. Это означает, что наблюдаемые различия статистически значимы на уровне значимости 0, 05 (5%), 0, 01(1%) или 0, 001 (0, 1%).
Вначале вычисляли величину среднего арифметического М по следующей формуле: М = 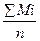 , где
, где 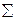 - символ суммы, Mi – значение отдельного измерения (варианта), n – общее число вариантов.
- символ суммы, Mi – значение отдельного измерения (варианта), n – общее число вариантов.
Далее определяли величину σ - среднее квадратическое отклонение по формуле: 
 .
.
Находили ошибку среднего арифметического - 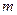 по формуле:
по формуле:
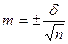 .
.
Параметрический t-критерий Стьюдента находили по формуле:
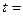
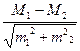
Следует учитывать, что число вариантов, и дисперсия в двух группах может быть как одинаково, так и нет, а для определения достоверности различия это необходимо учитывать. Учитывая данный факт, прежде чем оценить значение t-критерия Стьюдента, следует найти число степеней свободы v по следующим формулам:
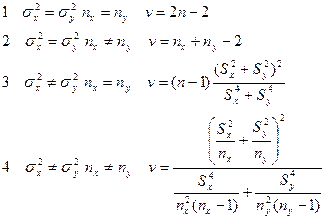
Далее полученное значение оценивается по таблице «t – распределение Стьюдента для оценки статической достоверности различий в группах”.
Критические значения двустороннего t – критерия Стьюдента
(v – число степеней свободы)
| Уровни значимости | |||||||||
| v | 0, 1 | 0, 05 | 0, 01 | 0, 001 | v | 0, 1 | 0, 05 | 0, 01 | 0, 001 |
| 6, 314 | 12, 706 | 63, 657 | 636, 619 | 1, 721 | 2, 080 | 2, 831 | 3, 819 | ||
| 2, 92 | 4, 308 | 9, 925 | 31, 599 | 1, 717 | 2, 074 | 2, 819 | 3, 792 | ||
| 2, 353 | 3, 182 | 5, 841 | 12, 924 | 1, 714 | 2, 069 | 2, 807 | 3, 768 | ||
| 2, 132 | 2, 776 | 4, 604 | 8, 610 | 1, 711 | 2, 064 | 2, 797 | 3, 745 | ||
| 2, 015 | 2, 571 | 4, 032 | 6, 869 | 1, 708 | 2, 060 | 2, 787 | 3, 725 | ||
| 1, 943 | 2, 447 | 3, 707 | 5, 959 | 1, 706 | 2, 056 | 2, 779 | 3, 707 | ||
| 1, 859 | 2, 365 | 3, 499 | 5, 408 | 1, 703 | 2, 052 | 2, 771 | 3, 690 | ||
| 1, 860 | 2, 306 | 3, 355 | 5, 041 | 1, 701 | 2, 048 | 2, 763 | 3, 674 | ||
| 1, 833 | 2, 262 | 3, 250 | 4, 781 | 1, 699 | 2, 045 | 2, 756 | 3, 659 | ||
| 1, 812 | 2, 228 | 3, 169 | 4, 587 | 1, 697 | 2, 042 | 2, 750 | 3, 646 | ||
| 1, 796 | 2, 201 | 3, 106 | 4, 437 | 1, 684 | 2, 021 | 2, 704 | 3, 551 | ||
| 1, 782 | 2, 179 | 3, 055 | 4, 318 | 1, 676 | 2, 009 | 2, 678 | 3, 505 | ||
| 1, 771 | 2, 160 | 3, 012 | 4, 221 | 1, 664 | 2, 000 | 2, 660 | 3, 505 | ||
| 1, 761 | 2, 145 | 2, 977 | 4, 140 | 1, 664 | 1, 990 | 2, 639 | 3, 416 | ||
| 1, 753 | 2, 131 | 2, 947 | 4, 073 | 1, 660 | 1, 984 | 2, 626 | 3, 391 | ||
| 1, 746 | 2, 120 | 2, 921 | 4, 015 | 1, 658 | 1, 980 | 2, 617 | 3, 373 | ||
| 1, 170 | 2, 110 | 2, 898 | 3, 965 | 1, 653 | 1, 972 | 2, 601 | 3, 340 | ||
| 1, 734 | 2, 101 | 2, 878 | 3, 922 | 1, 648 | 1, 965 | 2, 586 | 3, 310 | ||
| 1, 729 | 2, 093 | 2, 861 | 3, 883 | ∞ | 1, 645 | 1, 960 | 2, 580 | 3, 291 | |
| 1, 725 | 2, 086 | 2, 845 | 3, 850 | ||||||
| 0, 9 | 0, 95 | 0, 99 | 0, 999 | 0, 9 | 0, 95 | 0, 99 | 0, 999 | ||
| Доверительные уровни |
Примечание. Таблица составлена по Л.Н. Большеву и Н.В. Смирнову, 1968; М.Дж. Кендаллу и А.М. Стьюарту, 1973.