
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементарные функции и конформные отображения
|
|
Изучаемые вопросы: Линейная ФКП. Геометрический смысл производной. Дробно-линейная, показательная, логарифмическая, тригонометрические и гиперболические ФКП.
Простейшей из рассматриваемых элементарных ФКП является линейная:
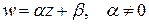 , (4)
, (4)
являющаяся формальным аналогом линейной функции вещественного переменного 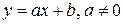 . Но вещественная функция ставит в соответствие точкам оси
. Но вещественная функция ставит в соответствие точкам оси 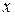 точки оси
точки оси 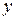 , т.е. осуществляет отображение
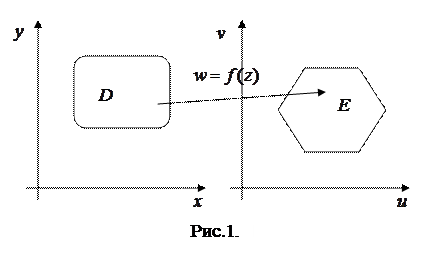
, т.е. осуществляет отображение 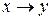 , а ФКП (4) отображает точки комплексной плоскости
, а ФКП (4) отображает точки комплексной плоскости 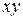 в точки комплексной плоскости
в точки комплексной плоскости 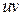 (рис.1).
(рис.1).
 Пусть
Пусть 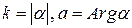 , т.е.
, т.е.
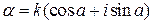 , тогда (4) можно представить как сложную функцию, составленную из функций
, тогда (4) можно представить как сложную функцию, составленную из функций
1) 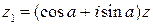 ;
;
2) 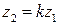 ;
;
3)  ;
;
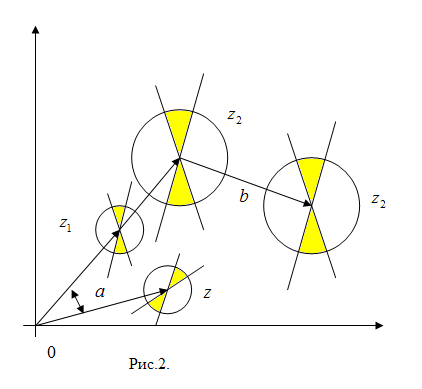
Видим (рис.2), что 1) отображает поворот вектора 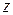 на угол
на угол 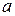 , изображаемый вектором
, изображаемый вектором 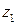 , 2) – отображает подобное преобразование вектора
, 2) – отображает подобное преобразование вектора 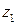 в вектор
в вектор 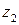 с коэффициентом подобия
с коэффициентом подобия 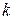 , а 3) – отображает сдвиг
, а 3) – отображает сдвиг 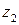 на постоянную величину
на постоянную величину 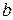 . Суперпозиция этих трёх преобразований и даёт в итоге вектор
. Суперпозиция этих трёх преобразований и даёт в итоге вектор 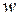 .
.
Пусть 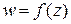 имеет в точке
имеет в точке 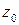 конечную производную
конечную производную 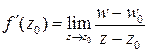 . Переменная, стремящаяся к конечному пределу, отличается от него на бесконечно малую:
. Переменная, стремящаяся к конечному пределу, отличается от него на бесконечно малую:
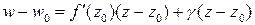 , (5)
, (5)
 где
где 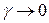 при
при 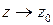 . В (5)
. В (5) 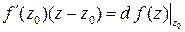 , и пусть
, и пусть
 , (6)
, (6)
тогда
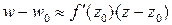 . (7) (5.9)
. (7) (5.9)
Последнее выражение показывает, что любое дифференцируемое отображение в окрестности фиксированной точки приближённо можно считать линейным, если выполняется условие (6). Отсюда вытекает геометрический смысл производной от ФКП: в малой окрестности точки 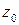 происходит подобное преобразование с коэффициентом
происходит подобное преобразование с коэффициентом 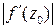 и поворот на угол
и поворот на угол 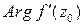 . Такое преобразование называется конформным в точке
. Такое преобразование называется конформным в точке 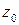 . Достаточным условием этого является условие (6).
. Достаточным условием этого является условие (6).
Отображение называется конформным в области, если оно взаимнооднозначно и конформно в каждой точке области. Заметим, что при конформном отображении, отличном от линейного, коэффициент подобия и угол поворота меняется от точки к точке.
Об остальных функциях Вы прочтёте Учебном пособии. Здесь лишь заметим, что, в отличие от функций вещественного переменного, показательная ФКП является периодической с периодом  , логарифмическая – бесконечнозначной, и что формально формулы дифференцирования элементарных ФКП совпадают с оными для функций вещественного переменного.
, логарифмическая – бесконечнозначной, и что формально формулы дифференцирования элементарных ФКП совпадают с оными для функций вещественного переменного.
Вопросы для самопроверки по теме 2.3
1. В чём состоит геометрический смысл производной от ФКП?
2. Напишите формулы элементарных ФКП: линейной, дробно-линейной, показательной, логарифмической.
3. В чём отличие вещественной и комплексной логарифмических функций?
4. Напишите равенство Эйлера.
5. Как выражаются тригонометрические функции вещественной переменной через показательную функцию?