
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычеты функций и их применение
|
|
Изучаемые вопросы: Теорема Коши о вычетах; Вычисление вычетов; Вычет в бесконечно удалённой точке; Приложение вычетов к вычислению интегралов.
2.6.1. Теорема Коши о вычетах
Пусть 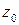 – изолированная особая точка функции
– изолированная особая точка функции 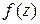 . В окрестности этой точки
. В окрестности этой точки 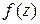 может быть представлена рядом Лорана
может быть представлена рядом Лорана
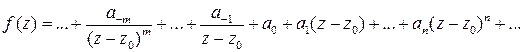 . (1)
. (1)
Коэффициент 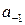 в разложении (1) называется вычетом функции
в разложении (1) называется вычетом функции 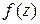 в изолированной особой точке
в изолированной особой точке 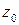 . Он обозначается как
. Он обозначается как
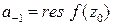 . (2)
. (2)
Теорема Коши. Если 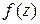 регулярна в области
регулярна в области 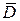 всюду, за исключением внутренних точек
всюду, за исключением внутренних точек 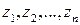 , то интеграл от функции
, то интеграл от функции 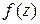 , взятый по контуру области
, взятый по контуру области 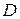 в положительном направлении, равен произведению
в положительном направлении, равен произведению 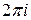 на сумму вычетов
на сумму вычетов 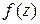 в точках
в точках 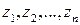 :
:
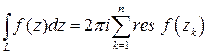 . (3)
. (3)
○ Исключим точки 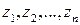 , окружив их достаточно малыми окрестностями с границами
, окружив их достаточно малыми окрестностями с границами 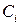 (см. рисунок).
(см. рисунок).
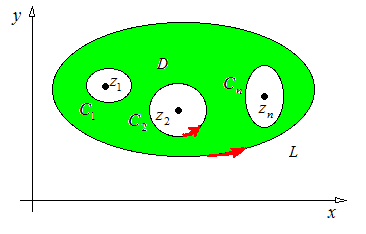 В оставшейся области
В оставшейся области 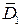 (она закрашена серым)
(она закрашена серым) 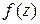 удовлетворяет всем условиям интегральной теоремы Коши, следовательно,
удовлетворяет всем условиям интегральной теоремы Коши, следовательно,
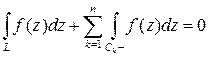 (4)
(4)
(здесь у контуров 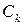 поставлен минус, т.к. обход окружностей осуществляется в отрицательном направлении – область
поставлен минус, т.к. обход окружностей осуществляется в отрицательном направлении – область 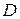 остаётся справа).
остаётся справа).
Но в окрестности 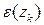 ряд Лорана для
ряд Лорана для 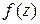 :
:
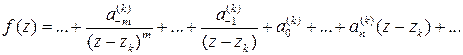 , (5)
, (5)
и, интегрируя почленно, получаем:
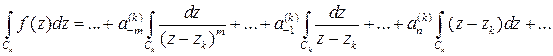 .
.
В этом интеграле все члены, кроме содержащего 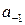 , равны нулю (см. п.2.4.4), а
, равны нулю (см. п.2.4.4), а
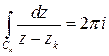 . (6)
. (6)
Изменив в (4) направление обхода, с учётом (6.) получим (3). ●
2.6.2. Вычисление вычетов
1. Рассмотрим вычисление вычета в полюсе первого порядка (простой полюс). Пусть в окрестности 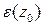 имеет место разложение
имеет место разложение
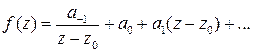 . (7)
. (7)
Умножим обе части этого равенства на 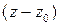 :
:
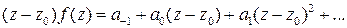 . (8)
. (8)
Устремим 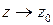 , тогда переходя к пределу, получаем
, тогда переходя к пределу, получаем
 . (9)
. (9)
Выражению (9) можно придать другой вид, если представить 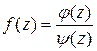 , где
, где 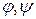 – регулярные в
– регулярные в 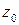 функции, причём
функции, причём 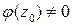 , а
, а 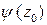 имеет простой корень. Тогда
имеет простой корень. Тогда 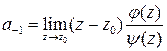 и, по правилу Лопиталя
и, по правилу Лопиталя
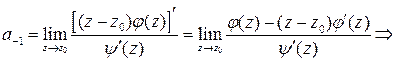
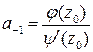 . (10)
. (10)
2. Пусть теперь 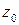 – полюс порядка
– полюс порядка 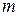 , т.е. ряд Лорана функции
, т.е. ряд Лорана функции 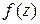 :
:
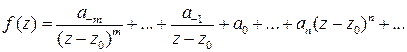 . (11)
. (11)
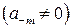 . Умножим обе части этого равенства на
. Умножим обе части этого равенства на 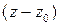 и продифференцируем по
и продифференцируем по 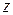
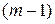 раз:
раз:
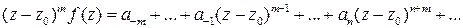 и устремим
и устремим 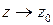
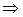
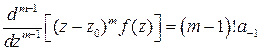 , (12)
, (12)
откуда, по аналогии с предыдущим пунктом,
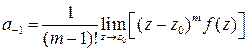 . (13)
. (13)
Пример 1. □ Найти вычеты 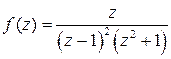 в изолированных особых точках.
в изолированных особых точках.
□ Полюсы функции 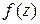 расположены в точках, в которых знаменатель дроби обращается в нуль, т.е. их можно найти, решив уравнения
расположены в точках, в которых знаменатель дроби обращается в нуль, т.е. их можно найти, решив уравнения 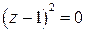 и
и 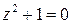 . Корни второго уравнения:
. Корни второго уравнения: 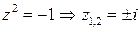 – простые полюсы, а корень первого уравнения
– простые полюсы, а корень первого уравнения 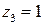 – полюс второго порядка (он равен степени разности
– полюс второго порядка (он равен степени разности 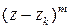 ). По формуле (6.9 из Учебного пособия) находим:
). По формуле (6.9 из Учебного пособия) находим:
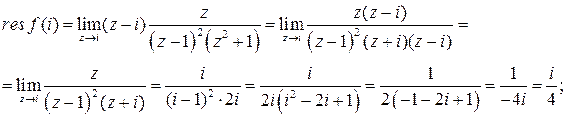
Аналогично, найдём, что 
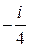 . В полюсе второго порядка по (13)
. В полюсе второго порядка по (13)
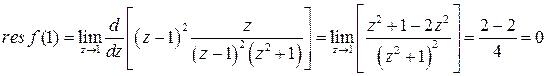 . ■
. ■
2.6.3. Вычет в бесконечно удалённой точке
Пусть в окрестности бесконечно удалённой точки 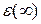 функция
функция 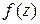 представима рядом Лорана
представима рядом Лорана
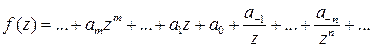 . (14)
. (14) 
Вычетом в бесконечно удалённой точке называется взятый с противоположным знаком коэффициент при минус первой степени 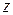 в разложении (14):
в разложении (14):
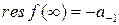 . (15)
. (15)
Пример 2. Найти вычет в бесконечности функции 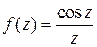 .
.
□ Разложение 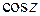 в степенной ряд
в степенной ряд 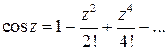 справедливо при любом
справедливо при любом 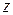 . Тогда
. Тогда 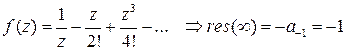 . ■
. ■
Теорема. Если 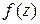 имеет конечное число особых точек, то сумма вычетов её, включая вычет в бесконечно удалённой точке, равна нулю, т.е.
имеет конечное число особых точек, то сумма вычетов её, включая вычет в бесконечно удалённой точке, равна нулю, т.е.
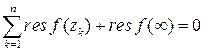 . (16)
. (16)
2.6.4. Приложение вычетов к вычислению интегралов
Если 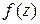 регулярна в односвязной области
регулярна в односвязной области 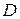 , то по теореме Коши интеграл от неё по любому замкнутому контуру в
, то по теореме Коши интеграл от неё по любому замкнутому контуру в 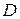 равен нулю:
равен нулю: 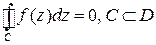 .
.
Основная теорема о вычетах: если 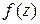 непрерывна на границе
непрерывна на границе 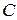 области
области 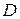 , за исключением конечного числа особых точек
, за исключением конечного числа особых точек 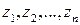 , то
, то
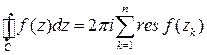 . (17)
. (17)
Для вычисления этого интеграла необходимо:
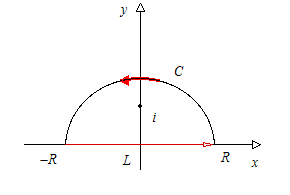
1. Определить контур интегрирования и сделать его рисунок.
2. Найти особые точки подынтегральной функции, которые находятся внутри контура интегрирования, и вычислить вычеты в них, определив тип этих точек.
3. Используя основную теорему о вычетах, найти численное значение интеграла.
Пример 1. Найти несобственный интеграл 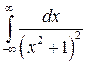 (
(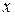 – вещественная переменная).
– вещественная переменная).
□ Рассмотрим интеграл от ФКП 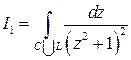 , где
, где 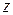 – комплексная переменная,
– комплексная переменная, 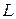 – отрезок вещественной оси,
– отрезок вещественной оси, 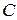 – полуокружность радиуса
– полуокружность радиуса 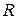 . Вычислим
. Вычислим 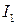 с помощью вычетов.
с помощью вычетов.
 Подынтегральная функция
Подынтегральная функция 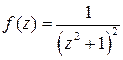 имеет полюсы второго порядка в точках
имеет полюсы второго порядка в точках 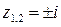 . Пусть
. Пусть 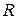 достаточно велико, так что
достаточно велико, так что 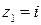 попадает внутрь контура (см. рисунок). Тогда для полюса второго порядка, который изображен на рисунке
попадает внутрь контура (см. рисунок). Тогда для полюса второго порядка, который изображен на рисунке
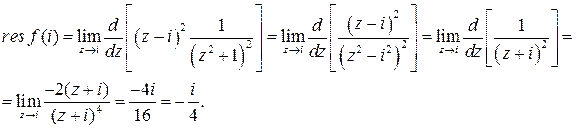
Следовательно, 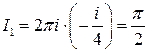 . С другой стороны,
. С другой стороны, 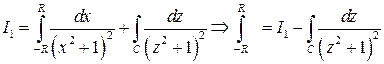 , а последний интеграл
, а последний интеграл 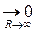 , и, значит,
, и, значит, 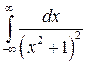
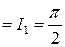 . ■
. ■
Вопросы для самопроверки по теме 2.6
1. Какой коэффициент ряда Лорана называется вычетом функции 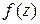 ?
?
2. Сформулируйте теорему Коши о вычетах.
3. Напишите формулы для вычисления вычетов в полюсе первого порядка, полюсе порядка 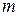 и в БУТ.
и в БУТ.
4. Чему равна сумма вычетов функции 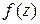 , имеющей конечное число особых точек?
, имеющей конечное число особых точек?
Все шесть тем этого раздела подробно описаны в Учебном пособии, которое Вам предстоит изучить. В результате Вы сможете решить задачи контрольной работы, варианты которой, в соответствии с вашим шифром, содержатся в разделе 4.