Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 2. Приближенное решение уравнений.
|
|
Приближенное решение уравнений.
Отделение корней. Уточнение корней.
1. Цель работы
Ознакомиться с численными методами решения конечных уравнений.
2. Основные теоретические положения
2.1. Постановка задачи
В общем случае уравнение с одним неизвестным имеет вид
f (x)=0, (7)
где f (х) – заданная функция, определенная на отрезке [ a, b ]. Всякое число x (действительное или мнимое) на отрезке [ a, b ], обращающее уравнение в тождество:
f (x)є0 (8)
называется корнем уравнения или его решением.
Решение задачи приближенного определения корней уравнения состоит из двух этапов:
1) отделение корней, т.е. нахождение подинтервалов [a, b] на отрезке [ a, b ], которые содержат только один корень уравнения;
2) уточнение корней, т.е. непосредственное вычисление значений корней на найденных подинтервалах [a, b] с заданной точностью e.
2.2. Отделение корней
Графический способ отделения корней заключается в построении графика функции f (x) на отрезке [ a, b ]. Точка пересечения графика функции с осью абсцисс дает приближенное значение корня уравнения. Найденные таким образом приближенные значения корней позволяют выделить отрезки [a, b], на которых при необходимости можно выполнить уточнение корней (рис.1).
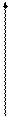
f (x)
x1 x2 x3
a1 b1 a2 b2 a3 b3 х
Рис. 1
При отделении действительных корней расчетным путем для непрерывных функций f (x) можно руководствоваться следующими соображениями:
если на концах отрезка [ a, b ] функция имеет разные знаки (f (a)× f (b)< 0), то между точками а и b на оси абсцисс имеется нечетное число корней;
если же f (a)× f (b)> 0, то между а и b имеется четное число корней или их совсем нет;
если f (a)× f (b)< 0 и либо первая производная f¢ (x), либо вторая производная f ¢ ¢ (x) не меняют знака на этом отрезке, то уравнение имеет единственный корень на отрезке [ a, b ].
2.3. Уточнение корней
Численный метод, при котором уточняется первоначальное грубое приближение, называется итерационным методом или методом последовательных приближений. Каждый шаг этого метода называется итерацией.
Если при последовательных итерациях (к = 1, 2,...) получаемые величины х (к) все ближе приближаются к истинному значению корня x, то итерационный процесс будет сходящимся, в противном случае – расходящимся. При этом различают монотонную и колебательную сходимость (расходимость) в зависимости от того, с одной или с разных сторон осуществляется приближение (удаление) к (от) искомому решению.
Для реализации итерационного процесса должны быть заданы начальное приближение х (0 ) и точность e, с которой требуется найти решение уравнения. Первоначальное грубое приближение х (0 ) следует задавать из физических соображений и по результатам отделения корней. Все остальные приближения получаются из итерационной формулы, соответствующей используемому методу решения уравнения.
Условие окончания итерационного процесса (нахождения значения корня с точностью e) имеет вид
Ѕ x ( к +1) - x ( к )Ѕ = < e, k = 0, 1, 2, 3, …. (9)
2.3.1 Уточнение корней Методом Ньютона
Опишем процедуру уточнения корня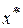 
, который отделён и находится на отрезке 
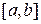. Уточнение корня проведём, используя итерационную формулу Ньютона
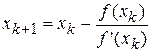, (10)
где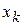 
– приближение к корню на k- ом шаге (на k- ой итерации), 
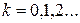. В пределе: 
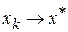при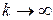 
.
Начальное приближение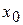 
– это любая точка из отрезка 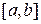, удовлетворяющая условию сходимости итерационного процесса (1)
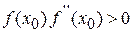. (11)
Обычно в качестве значения 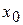используют либо левый, либо правый конец отрезка .
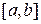Пример 1.
Уточнить корень уравнения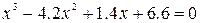 
на отрезке 
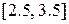, сделав три шага по формуле Ньютона.
○ Вычислим первую и вторую производные функции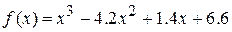 
. Получим 
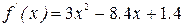и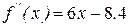 
.
Итерационное уравнение в нашем случае запишется так
,
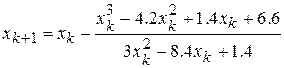или после приведения дробей к общему знаменателю в правой части последнего соотношения, получим более удобное для дальнейших вычислений уравнение
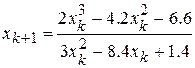. (12)
В качестве начального приближения возьмём правый конец отрезка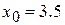 
.
Проверяем условие сходимости (11)
.
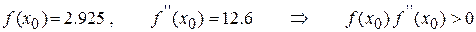Условие сходимости метода Ньютона для 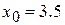выполнено. Последовательно применяя соотношение (3), получим:
; 
;
.
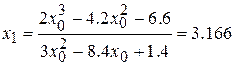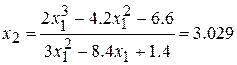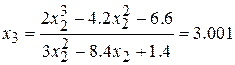Уточнённое значение корня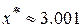 
.
В качестве оценки абсолютной погрешности, полученного результата можно использовать величину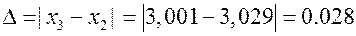 
.●