
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 4. Приближенное интегрирование дифференциальных уравнений 1 –го порядка методом Эйлера Цель работы
|
|
Приближенное интегрирование дифференциальных уравнений 1 –го порядка методом Эйлера
- Цель работы
Изучение метода Эйлера интегрирования дифференциальных уравнений 1 – го порядка.
- Основные теоретические положения
Согласно методу Эйлера для решения дифференциального уравнения 1-го порядка
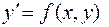 (20)
(20)
с начальным условием
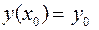 (21)
(21)
(так называемая задача Коши) отрезок [ a, b ], на котором ищется решение задачи, разбивают на n частей с шагом h = (b – a) / n и находят значения
yk = y (xk) в точках xk = x0 + k× h (k = 0, 1,.. n). Очевидно, что при этом x 0 = a, xn = b. Значения yk+1 определяется по формуле
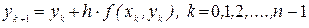 , (22)
, (22)
которая получается заменой производной на ее разностный аналог.
Погрешность вычислений на каждом шаге составляет
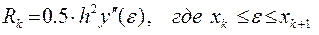 (23)
(23)
Пример 1.
Решить задачу Коши для обыкновенного дифференциального уравнения 1-го порядка методом Эйлера. Вычисления выполнять с четырьмя десятичными знаками на отрезке [0, 2; 1, 2] с шагом 0, 1. Уравнение:
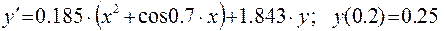
○ Для численного решения заданного уравнения с начальным условием нам потребуется выполнить 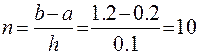 шагов. На каждом шаге надо вычислить значения
шагов. На каждом шаге надо вычислить значения 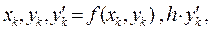 и
и 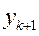 .
.
Первый шаг. (k = 0). Имеем:
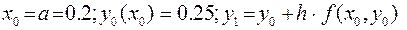 . Вычислим
. Вычислим
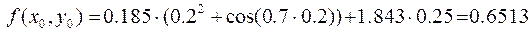 .
.
Тогда 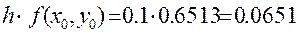 и, следовательно, по формуле (22)
и, следовательно, по формуле (22)
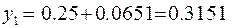 .
.
Делаем следующий шаг.
Второй шаг. (k= 1).
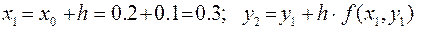 .
.
Вычислим 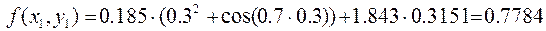 .
.
Тогда 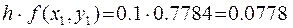 и
и 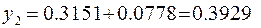 .
.
И так далее.
Для удобства, все вычисления удобно представить в виде таблицы
| k | xk | yk | y`k=f(xk, yk) | h× yk | yk+1 |
| 0, 2 | 0, 25 | 0, 6513 | 0, 0651 | 0, 3151 | |
| 0, 3 | 0, 3151 | 0, 7784 | 0, 0778 | 0, 3929 | |
| 0, 4 | 0, 3929 | 0, 9316 | 0, 0932 | 0, 4861 | |
| 0, 5 | 0, 4861 | 1, 1160 | 0, 1116 | 0, 5977 | |
| 0, 6 | 0, 5977 | 1, 3371 | 0, 1337 | 0, 7314 | |
| 0, 7 | 0, 7314 | 1, 6019 | 0, 1602 | 0, 8916 | |
| 0, 8 | 0, 8916 | 1, 9184 | 0, 1918 | 1, 0835 | |
| 0, 9 | 1, 0835 | 2, 2962 | 0, 2296 | 1, 3131 | |
| 1, 0 | 1, 3131 | 2, 7466 | 0, 2747 | 1, 5878 | |
| 1, 1 | 1, 5878 | 3, 2829 | 0, 3283 | 1, 9161 | |
| 1, 2 | 1, 9161 | 3, 2912 | 0, 3291 |
Таким образом, задача решена. ●