
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коническая поверхность
|
|
Коническая поверхность моделируется образующей прямой, проходящей через общую точку (вершину) и перемещающейся по направляющей кривой (плоской или пространственной).



 а) l S
а) l S

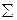
 |

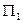 m
m






 б) S
б) S  в) S
в) S 
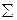

 l
l 







 m
m 
 | |||||
 |  |

 S
S 
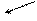

 l
l  S
S  m
m 

Рис. 6.5
Аксонометрический чертёж такой поверхности представлен на рис.6.5а, комплексный чертёж её определителя – на рис. 6.5б, чертёж очерка конической поверхности – на рис. 6.5в.
Частный случай конической поверхности – конус вращения (рис. 6.6).
 |

 S
S 


 m
m 
 |
S 
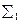 m
m 
Рис 6.6
1.3. Поверхности вращения с прямолинейными образующими
В зависимости от взаимного положения образующей и оси вращения различают следующие варианты поверхностей.
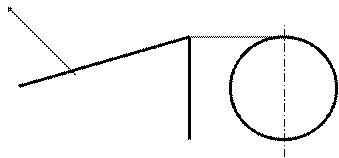
1. Цилиндрвращения 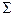 (l || i), представленный на рис. 6.7.
(l || i), представленный на рис. 6.7.
2. Конусвращения 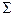 (l
(l 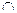 i), см. рис. 6.8.
i), см. рис. 6.8.
3. Однополостныйгиперболоидвращения 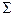 (l
(l 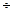 i), см. рис. 6.9.
i), см. рис. 6.9.



 l
l 
 l
l 
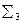
 |

 i
i  i
i 
 |
Рис. 6.7


 l
l 
 l
l 

 S
S 

 |

i  S
S  = i
= i 

Рис. 6.8
 l
l  i
i 
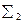
 |  |

i  l
l 
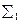
а) Чертёж определителя однополостного б) Очерковый чертёж поверхно-
гиперболоида вращения 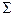 (l
(l 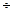 i). сти
i). сти 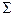 (l
(l  i).
i).
Рис. 6.9
1.5. Винтовые поверхности с прямолинейными образующими (геликоиды)
Эти поверхности моделируют винтовым движением образующей, пересекающей направляющие: винтовую линию и ось вращения. Образующая совершает при этом сложное движение: вращательное вокруг оси и поступательное вдоль оси, одновременно.
Если угол между образующей и осью вращения равен 90 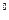 , то при моделировании получают прямой геликоид, у которого имеется плоскость параллелизма, перпендикулярная оси вращения. Все образующие прямого геликоида параллельны этой плоскости.
, то при моделировании получают прямой геликоид, у которого имеется плоскость параллелизма, перпендикулярная оси вращения. Все образующие прямого геликоида параллельны этой плоскости.
Если угол между образующей и осью вращения не равен 90 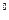 , то получают косой геликоид, у которого имеется конус параллелизма, при этом оси вращения этого конуса и геликоида совпадают, а все образующие конуса параллельны соответствующим образующим косого геликоида.
, то получают косой геликоид, у которого имеется конус параллелизма, при этом оси вращения этого конуса и геликоида совпадают, а все образующие конуса параллельны соответствующим образующим косого геликоида.
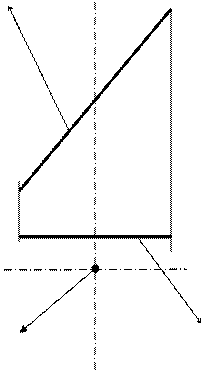
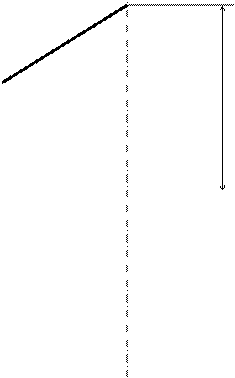
На рис. 6.10 приведён чертёж элементов определителя косого геликоида и его конус параллелизма  .
.
Винтовые поверхности используют при образовании резьбовых поверхностей деталей машин.
 |
 l
l  i
i  Ход винтовой линии
Ход винтовой линии
 | |||||||
 | |||||||
 | |||||||
 | |||||||



 | |||
 | |||
 |
l  i
i 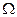

i 
Рис. 6.10