
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциальные уравнения первого порядка
|
|
Дифференциальное уравнение первого порядка имеет вид
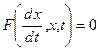
или
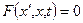 .
.
Дифференциальные уравнения классифицируются как
· Линейные, например 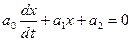 ;
;
· нелинейные, например 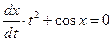 .
.
В свою очередь линейные ДУ делятся на
· однородные 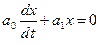 ;
;
· неоднородные 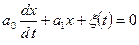 , где
, где 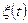 - произвольная непрерывная функция времени. Если
- произвольная непрерывная функция времени. Если 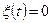 , уравнение становится однородным.
, уравнение становится однородным.
Если ДУ первого порядка 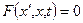 , можно разрешить относительно
, можно разрешить относительно 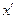 , то, как правило, оно представляется в виде
, то, как правило, оно представляется в виде
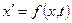 . .
| (7.10) |
Для непрерывных в некоторой области функций 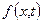 и
и 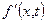 уравнение (7.10) имеет бесконечное множество решений. Общим решением уравнения (7.10) является некоторая функция
уравнение (7.10) имеет бесконечное множество решений. Общим решением уравнения (7.10) является некоторая функция 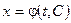 .
.
Существует частное решение 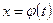 уравнения (7.10), удовлетворяющее условию
уравнения (7.10), удовлетворяющее условию
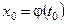 . .
| (7.11) |
Числа 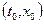 называются начальными значениями для решения
называются начальными значениями для решения 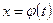 , а соотношение (7.11) - начальным условием этого решения. Решение
, а соотношение (7.11) - начальным условием этого решения. Решение 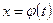 , удовлетворяющее начальным значениям
, удовлетворяющее начальным значениям 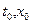 , называется частным решением ДУ.
, называется частным решением ДУ.
Линейное однородное дифференциальное уравнение первого порядка имеет вид
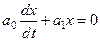 . .
| (7.12) |
.
Относительно производной 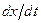 уравнение (7.12) преобразуется к виду
уравнение (7.12) преобразуется к виду
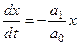
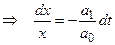 .
.
Общее решение этого уравнения с разделяющимися переменными
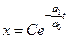 , ,
| (7.13) |
где С - произвольное действительное число.
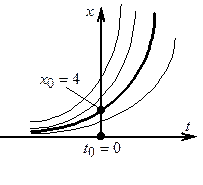 Геометрически на плоскости общее решение ДУ (рис. 7.10) представляется семейством кривых, каждая из которых соответствует различным начальным условиям.
Геометрически на плоскости общее решение ДУ (рис. 7.10) представляется семейством кривых, каждая из которых соответствует различным начальным условиям.
Пример. Найти общее и частное решение дифференциального уравнения 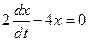 при заданных начальных значениях
при заданных начальных значениях 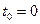 ,
, 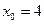 .
.
Преобразуем уравнение к виду (7.10): 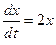 .
.
| Рис. 7.10. Решение ДУ |
Общее решение 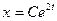
По условию известно, что при 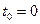 ,
, 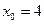 , тогда
, тогда 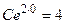 , откуда
, откуда 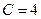 . Частное решение исходного ДУ
. Частное решение исходного ДУ 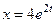 .
.