
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 5
|
|
По пяти однотипным предприятиям (табл.7) имеются следующие данные о выпуске продукции (х) в тыс. ед. и о расходе условного топлива (y) в тоннах.
Таблица 7- Данные о выпуске продукции и расходе топлива
| х. | |||||
| y |
С помощью линейного коэффициента корреляции определить наличие связи между расходом топлива и выпуском продукции.
Решение:
1. Построим макет таблицы
| х | y | 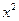
| 
| хy |
r =  =
= 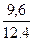 = 0.77
= 0.77
Вывод: Связь между выпуском продукции и расходом топлива – сильная.
4. Ряды динамики.
Ряды динамики – это ряды с изменяющимися во времени значениями статистических показателей, расположенных в хронологическом порядке.
Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (года, кварталы, месяцы, сутки) или моменты (даты) времени.
Уровни ряда обычно обозначаются через “у”, моменты или периоды времени, к которым относятся уровни, - через “t ”.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся:
- абсолютный прирост;
- темп роста;
- темп прироста.
Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение - базисным.
Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо первоначальный уровень, в ряду динамики, либо какой-то новый этап развития явления. Такие показатели называются базисными.
Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа называются цепными.
Абсолютный прирост (сокращение) характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени.
Для характеристики интенсивности, т.е. относительного уменьшения, уровня динамического ряда за к.л. период времени, исчисляют темпы роста (снижение). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.
Показатель интенсивности изменения уровня ряда выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели изменения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение.
Темп роста всегда представляет собой положительное число.
Относительную оценку скорости измерения уровня ряда динамики в единицу времени дают показатели темпа прироста (сокращения).
Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.
Темп прироста может быть положительным, отрицательным или равным нулю, и выражается в процентах или долях единицы (коэффициент прироста).
Показатели изменения уровней ряда динамики могут быть исчислены по формулам
Абсолютный прирост
Цепной Базисный
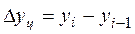 ,
,  ,
,
где yi – уровень сравниваемого периода;
yi-1 – уровень предшествующего периода;
y0 – уровень базисного периода.
Коэффициент роста
Цепной Базисный
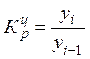 ,
,  .
.
Темп роста (сокращения)
цепной Базисный
 ,
, 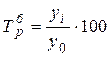 .
.
Темп прироста (сокращения)
Цепной Базисный
 ,
, 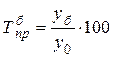 .
.
или
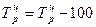
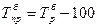
Коэффициент прироста
 ,
, 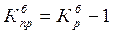 .
.
Средний абсолютный прирост (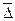 у) – обобщающая характеристика ряда динамики, служащая для сравнения скорости развития разных рядов. Показатель определяется по формуле
у) – обобщающая характеристика ряда динамики, служащая для сравнения скорости развития разных рядов. Показатель определяется по формуле
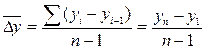 ,
,
где уn – последнее значение уровня ряда динамики;
у1 – первое значение уровня ряда;
n – число уровней ряда.
Средний коэффициент ростапоказывает, во сколько раз в среднем за единицу времени изменится уровень ряда динамики.
 ;
; 
Средний темп прироста (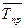 )характеризует среднюю интенсивность изменения уровней ряда динамики
)характеризует среднюю интенсивность изменения уровней ряда динамики
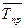 =
=  – 100% = (kр – 1) ∙ 100%
– 100% = (kр – 1) ∙ 100%
и является сводной характеристикой развития явления.