Модифікації методу Ейлера

З метою підвищення точності методу Ейлера використовують різні його модифікації.

Суть удосконаленого методу Ейлера полягає в використанні ітераційної формули виду:

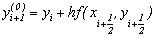, (9.16)

де 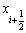- значення аргументу х в точці 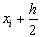, а 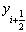- значення функції в точці .

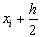Розглянемо диференціальне рівняння

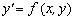(9.17)

Алгоритм методу складається з:

1. визначення похідної 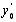в точці :

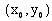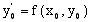
2. змінна х за формулою:

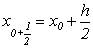
3. визначення значення 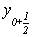при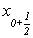

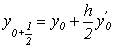
4. визначення похідної в точці (, )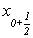

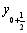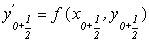
5. використовуємо отримане значення 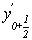для визначення 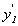за формулою:

,

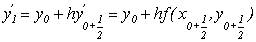6. змінюємо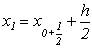

7. повторюємо всі кроки алгоритму, починаючи з першого.

Модифікований метод Ейлера заснований на використанні ітераційної формули виду:

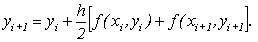(9.19)

Алгоритм методу включає наступні кроки:

1. визначення похідної 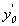в точці :

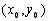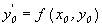
2. зміна незалежної змінної х за формулою:

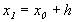
3. визначення проміжного значення 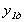за формулою методу Ейлера

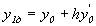
4. визначення проміжної похідної в точці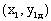

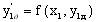
5. визначення середньо арифметичного значення двох похідних

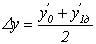
6. визначення у₁ за формулою

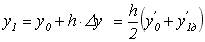
ітераційний процес повторюється, починаючи з першого кроку.

Удосконалений метод Ейлера - Коші з наступною ітераційною обробкою. Метод Ейлера - Коші з ітераційною обробкою є більш точним, чим, раніше розглянутий метод Ейлера - Коші. Сутність його полягає в тім, що виробляється ітераційна обробка кожного знайденого значення y_і. Спочатку вибирається грубе наближення потім будується ітераційний процес:

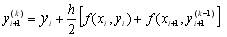(9.20)

Ітерації продовжуються доти, поки два послідовних наближення не збіжаться до заданої похибки. Після цього приймається 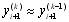. Якщо після трьох-чотирьох ітерацій, при обраному значенні h, збігу потрібних знаків не відбувається, то варто зменшити крок розрахунку h.