Закон инерции квадратичной формы

Квадратичная форма может быть приведена к каноническому виду различными способами (методом Лагранжа, методом ортогональных преобразований или методом Якоби). Но, несмотря на многообразие канонических видов для данной квадратичной формы, имеются такие характеристики её коэффициентов, которые во всех этих канонических видах остаются неизменными. Речь идет о так называемых числовых инвариантах квадратичной формы. Одним из числовым инвариантом квадратичной формы является ранг квадратичной формы.

Теорема 6.4 ( об инвариантности ранга квадратичной формы ). Ранг квадратичной формы не меняется при невырожденных линейных преобразованиях и равен числу отличных от нуля коэффициентов в любом ее каноническом виде. Другими словами, ранг квадратичной формы равен количеству ненулевых собственных чисел матрицы квадратичной формы (с учетом их кратности).

Доказательство теоремы приведено в […].

Определение 6.10. Ранг квадратичной формы называется индексом инерции. Число 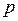положительных и число () отрицательных чисел в нормальном виде (3) квадратичной формы называются положительным и отрицательным индексами инерции квадратичной формы соответственно. При этом список называется сигнатурой квадратичной формы.

Положительный 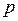и отрицательный индексы инерции являются числовыми инвариантами квадратичной формы. Справедлива теорема, называемая законом инерции.

Теорема 6.5 ( закон инерции ). Канонический вид (6.17) квадратичной формы определён однозначно, то есть сигнатура не зависит от выбора диагонализирующего базиса (не зависит от способа приведения квадратичной формы к каноническому виду).

□ Утверждение теоремы означает, что если одна и та же квадратичная форма при помощи двух неособенных линейных преобразований

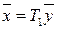, (6.21)

приведена к различным каноническим видам ():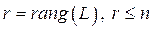

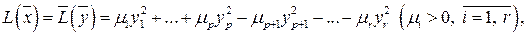
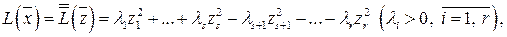
то обязательно 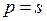, то есть количество положительных коэффициентов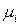 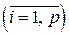совпадает с количеством положительных коэффициентов .

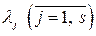Вопреки утверждению, предположим, что 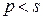. Так как преобразования (6.21) невырожденные, то выразим из них канонические переменные :

, .

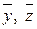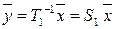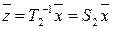Найдем вектор 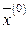такой, чтобы соответствующие векторы 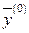, 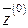имели вид

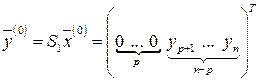, (6.22)

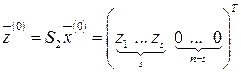. (6.23)

Для этого представим матрицы 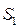и 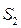в следующих блочных видах:

, ,

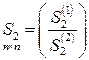где обозначены 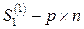-матрица, 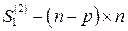-матрица, 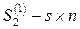-матрица, 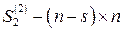-матрица.

В результате блочных представлений матриц 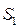и 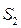составим однородную систему линейных алгебраических уравнений, взяв из (6.22) первые уравнений, а из (6.23) – последние 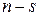уравнений:

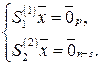
Полученная система содержит уравнений и 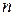неизвестных (компонент вектора 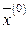). Так как 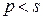, то 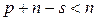, то есть в этой системе число уравнений меньше числа неизвестных, и она имеет бесконечное количество решений, среди которых можно выделить ненулевое решение .

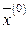На полученном векторе 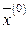значения формы имеют разные знаки:

,

,

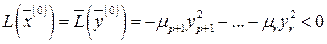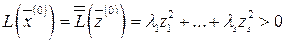что невозможно. Значит, предположение о том, что 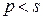неверно, то есть .

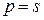Из того, что 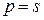следует, что сигнатура не зависит от выбора диагонализирующего базиса. ■

В качестве иллюстрации закона инерции можно показать, что квадратичная форма от трех переменных:

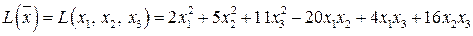
двумя неособенными линейными преобразования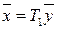ми , с соответствующими матрицами

,

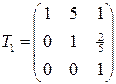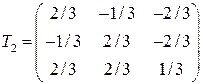
(первая матрица соответствует методу Лагранжа, вторая – методу ортогональных преобразований) приводится соответственно к двум различным каноническим формам

, .

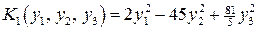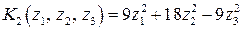При этом обе канонические формы имеют одну и ту же сигнатуру