Критерий Сильвестра

Тип квадратичной формы можно легко определить, не приводя ее к каноническому виду. Следующий ниже критерий Сильвестра позволяет определить тип квадратичной формы по знакам угловых миноров ее матрицы. Данный критерий напрямую связан с методом Якоби приведения квадратичной формы к каноническому виду.

Рассмотрим угловые миноры (), являющиеся определителями подматриц 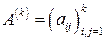матрицы 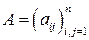квадратичной формы:

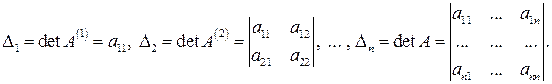
Теорема 6.8 (критерий Сильвестра знакоопределенности квадратичной формы).Квадратичная форма 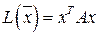является:

1) положительно определенной тогда и только тогда, когда все угловые миноры 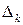матрицы положительны:

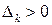() (6.24)

2) отрицательно определенной тогда и только тогда, когда все угловые миноры 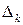матрицы отличны от нуля и их знаки чередуются, начиная со знака минус:

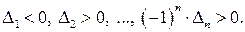(6.25)

□ 1.1. Необходимость. Покажем, что если форма, заданная матрицей в некотором базисе , является положительно определенной, то выполняются неравенства (6.24). Так как форма является положительно определенной, то положительный индекс инерции равен размерности пространства 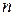. Тогда существует нормализующий базис , в котором квадратичная форма имеет нормальный вид

,

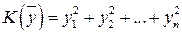а матрица этой квадратичной является единичной.

По формулам перехода от базиса к базису матрицы и связаны соотношениями

где . Так как , то имеем

,

откуда пользуясь свойствами определителей, получаем неравенство (6.24) для старшего углового минора:

.

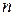Далее, так как форма от переменных 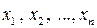является положительно определенной, то квадратичная форма

от переменных с матрицей

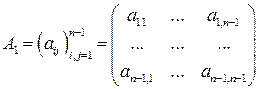
является положительно определенной. Значит, по доказанному выше её старший угловой минор положительный (он же совпадает с угловым минором ):

.

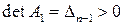Аналогично показывается, что все остальные угловые миноры также строго положительные.

1.2. Достаточность. Покажем, что если выполняются неравенства (6.24), то квадратичная форма является положительно определенной. Так как выполняются неравенства (6.24), то форма удовлетворяет условиям Якоби, то есть существует канонический базис, в котором форма имеет вид

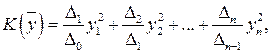
где все коэффициенты при квадратах переменных положительные, значит, по теореме 6.6 , и форма является положительно определенной.

2. Если форма является отрицательно определенной, то форма является положительно определенной. При этом матрицей формы является матрица 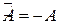, противоположная к матрице формы . Причем по свойствам определителей

().

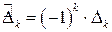Так как форма является положительно определенной, то по доказанному в пункте 1 этой теоремы знаки угловых миноров 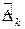() матрицы строго положительны

().

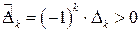Отсюда непосредственно вытекает справедливость неравенств (6.25). ■