Методы определения порядка реакции и константы скорости

В кинетике реакций простых и сложных типов решаются главным образом следующие задачи:

1. Прямая задача: известен порядок реакции и ее константа скорости. Требуется найти концентрацию какого-либо из исходных веществ или продуктов реакции в определенный момент времени или найти время, за которое концентрация какого-либо из реагентов или продуктов реакции достигает определенного значения.

2. Обратная задача: получены экспериментальные данные по кинетике ранее не изученной реакции. Требуется определить порядок реакции и константу скорости.

Для определения порядка реакции необходимо иметь экспериментальные данные об изменении концентрации реагирующих веществ со временем:

1. Метод подбора уравнений

Метод состоит в подстановке экспериментальных данных по концентрации веществ для каждого момента от начала реакции в кинетические уравнения различных порядков (этот прием ничего не дает, если порядок реакции превышает 3 или является дробным):

k = (с₀ - с) /t = x/t (нулевой порядок);

k = (1/t) lnс₀/с (первый порядок);

k = (1/t) x /с₀с ( второй порядок).

Порядок реакции будет соответствовать тому уравнению кинетики, для которого при различных начальных концентрациях исходных веществ и в различные моменты времени при заданной температуре константа скорости будет величиной постоянной.

2. Графические интегральные методы

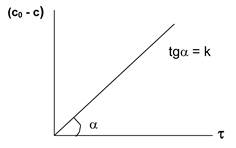
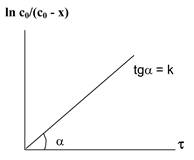
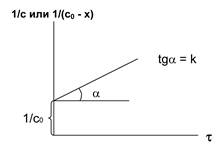
нулевой порядок: первый порядок второй порядок

Рис. 5.1. Изменение концентрации во времени для реакций различных порядков

 

Находят такую функцию от концентрации, отложив которую на графике, в зависимости от времени, получают прямую линию (рис. 5.1.).

3. По периоду полупревращения.

По зависимости периода полупревращения от начальной концентрации:

нулевой порядок: t_1/2 = с₀ /2k;

первый порядок: t_1/2 = 0, 693/ k;

второй порядок: t_1/2 = 1 / kс₀.

В общем виде:

t_1/2 ≈ 1 /k с₀ ^n-1.

Проводят опыты при двух различных начальных концентрациях (с₀)’ и (с₀)”:

(t_1/2)^’ = 1 /k (с₀)₁ ^n-1 (1)

(t_1/2)” = 1 /k (с₀)₂^n-1 (2)

Разделим (1) на (2):

(t_1/2)^’ / (t_1/2)” = (с₀)₂ ^n-1 / (с₀)₁ ^n-1.

Прологарифмируем:

lg(t_1/2)^’ / (t_1/2)” = (n-1) ´ lg[(с₀)₂ /(с₀)₁],

n = 1 + [lg(t_1/2)^’ - lg(t_1/2)”] / [lg(с₀)₂ - lg(с₀)₁].

4. Дифференциальный метод (метод Вант-Гоффа)

Используют зависимость скорости реакции от концентрации при условии равенства концентраций всех исходных веществ (рис. 5.2.): W = kсⁿ. Логарифмируем данное выражение: lgW = lgk + nlgс.

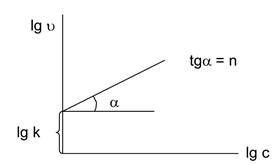
Рис. 5.2. Зависимость скорости реакции от концентрации

 

5. Интегральный метод Вант-Гоффа (по зависимости скорости реакции от начальной концентрации в первые моменты времени - 10-15 с).

W = k (c₀ - x)ⁿ = k c₀ ⁿ,

Так как в первый момент времени x ≈ 0.

Проводят опыт с различными начальными концентрациями.

W₁ = k c₁ ⁿ (1)

W₂ = k c₂ ⁿ (2)

Делим уравнение (1) на уравнение (2): W₁ /W₂ = (c₁/ c₂)ⁿ.

Логарифмируем:

n = (lgW₁ - lgW₂) / (lgс₁ -lgс₂),

где с₁ и с₂ берутся средними на исследуемом участке реакции, соответствующем Δ t.

6. Метод изолирования Оствальда

Запишем кинетическое уравнение реакции: W = kс _A ⁿ₁ ´ с _B ⁿ₂ ´ с _с ⁿ₃.

Увеличиваем концентрацию “В” и ”С” больше чем в 10 раз. Порядок по этим веществам будет нулевым, их концентрации не будут меняться. Определяем “n₁” одним из тех методов, которые были рассмотрены выше. Так же поступаем, определяя порядок реакции по веществам В и С, т.е. n₂ и n₃.