
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифракция на решетке
|
|
 l
l
 d
d






 q
q
q D = d sin(q)
Разность хода: D= d sin(q).
Условие главных минимумов: d sin(q) = ml
Дополнительных минимумов: d sin(q) =±(m¢ /N)× l,
m¹ pN p = 0, 1, 2.. (m не кратно числу штрихов решетки )
Условие главных максимумов: d sin(q) = ml, m£ d/l.
Где d – постоянная решетки;
m- порядок спектра;
q - угол дифракции;
l - длина волны падающих лучей.
Постоянная решетки (период решетки): d=1/N0,
N0= 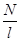 - число щелей на единицу длины решетки.
- число щелей на единицу длины решетки.
Разрешающая способность дифракционной решетки R = 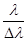 =m N,
=m N,
где N – общее число щелей,
m – порядок спектра,
l и l + Dl -длины волн двух близких спектральных линий.
Угловая дисперсия дифракционной решетки характеризует степень
пространственного (углового) разделения волн с различными длинами:
D = 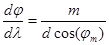 .
.
Единица измерения радиан на ангстрем, 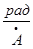 .
.
Линейная дисперсия дифракционной решетки:
D1 = f× D = 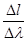 ,
,
где f – фокусное расстояние линзы, проецирующей спектр на экран.
Единица измерения миллиметр на ангстрем, 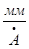 .
.
Задача 1.[И 5. I08].
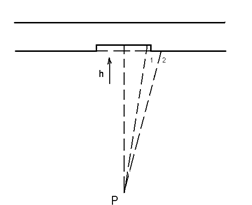
Плоская световая волна с λ = 0, 6 мкм падает нормально на достаточно большую стеклянную пластину, на противоположной стороне которой сделана круглая выемка. Для точки наблюдения Р она представляет собой первые полторы зоны Френеля. Найти глубину h выемки, при которой интенсивность света в течении Р будет:
а) максимальной,
б) минимальной,
в) равно интенсивности падающего света 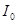 .
.
Чему равна интенсивность в точке Р в п.п. а) и б)?
Дано: Решение:
l = 0, 60 мкм
m = 1, 5 В задаче рассматривается дифракция Френеля
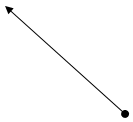
a)Imax -? Пользуясь методом Френеля, представим действие
б)Imin -? пластинки с выемкой на диаграмме Френеля. 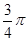
в)I=I0, h-?
 |  | ||
 - действие первых полутора зон (выемка).
- действие первых полутора зон (выемка).
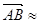
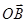 -действие остальной части пластинки. Т.к. m = 1, 5 – мало, то АВ
-действие остальной части пластинки. Т.к. m = 1, 5 – мало, то АВ 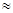 ОВ. Тогда D ОАВ прямоугольный равнобедренный и действия
ОВ. Тогда D ОАВ прямоугольный равнобедренный и действия 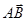 и
и 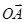 имеют сдвиг фаз» 3/4p в полностью открытом волновом фронте (без выемки). Из-за наличия выемки между
имеют сдвиг фаз» 3/4p в полностью открытом волновом фронте (без выемки). Из-за наличия выемки между 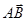 и
и 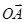 появляется дополнительная разность фаз за счет разности хода h(n-1). Связь разности хода D и разности фаз Dj устанавливается через модуль волнового вектора k = 2p/l, D =Dj / k.
появляется дополнительная разность фаз за счет разности хода h(n-1). Связь разности хода D и разности фаз Dj устанавливается через модуль волнового вектора k = 2p/l, D =Dj / k.
а) Максимум интенсивности будет иметь место при совпадении фаз действий выемки и остальной части, т.е. за счет разности хода должна вноситься дополнительная разность фаз, такая, чтобы действия были синфазны, т.е. Dj = 3/4p + 2pm, m =0, 1, 2,..
 Тогда
Тогда 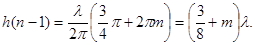


 3/4p Откуда
3/4p Откуда 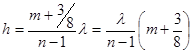 ;
;
А В
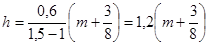 мкм.
мкм.
О
Интенсивность прямо пропорциональна квадрату амплитуды. Следовательно, I ~ (OA+AB)2.
Так как АВ 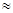 ОВ, то АВ2 ~ I, а ОА» ОВ
ОВ, то АВ2 ~ I, а ОА» ОВ 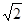 »АВ
»АВ 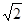
и I ~ (АВ 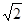 +АВ)2 ~ I0(
+АВ)2 ~ I0(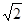 +1)= I0 (2
+1)= I0 (2 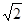 +3.)
+3.)
б) Минимум интенсивности будет иметь место при противофазности действий выемки и остальной части, т.о. разность хода должна обеспечивать разность фаз 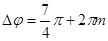 , где m = 0, 1, 2,..
, где m = 0, 1, 2,..




 2p А В 3/2p А В
2p А В 3/2p А В
Тогда  .
.
Откуда 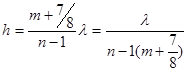 ;
;
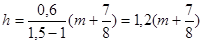 мкм.
мкм.
Аналогично пункту а) имеем для оценки интенсивности
I ~ (OA - AB)2 = (АВ 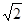 - АВ)2= I0(
- АВ)2= I0(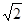 -1)= I0 (3-2
-1)= I0 (3-2 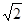 .).
.).
в) Та же интенсивность будет иметь место (интенсивность не изменится) в двух случаях.
Первый их них очевиден: вносимая разностью хода разность фаз составляет 2pm.
Тогда Dj = 2pm, m =1, 2,.. и 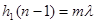 , откуда h1 =
, откуда h1 = 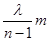 = 1, 2m мкм.
= 1, 2m мкм.
Второй, как видно из рисунка, имеет место при Dj = 3/2p + 2pm, m =0, 1, 2,..
Тогда 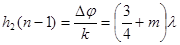 ,
,
Откуда 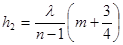 ,
,
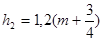 мкм.
мкм.
Ответ: а) 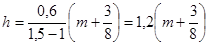 мкм, I = I0 (2
мкм, I = I0 (2 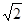 +3),
+3),
б) 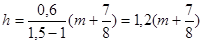 мкм, I = I0 (3-2
мкм, I = I0 (3-2 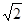 ),
),
в) h1 = 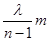 = 1, 2m мкм,
= 1, 2m мкм, 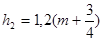 мкм.
мкм.
Задача 2./Ир5.126/
Свет с длиной волны l = 0, 50 мкм падает на щель ширины b =10 мкм под углом q = 300 к ее нормали. Найти угловое положение первых минимумов, расположенных по обе стороны центрального фраунгоферова максимума.
 Дано: Решение:
Дано: Решение:

 l = 0, 50 мкм
l = 0, 50 мкм
 b =10 мкм
b =10 мкм
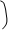
 q = 300 q q
q = 300 q q
 j -? j
j -? j
 m=± 1 j
m=± 1 j
В соответствии с дифракцией Фраунгофера на щели при нормальном падении света, разность хода лучей, идущих в точку минимума от краев щели, должна быть кратна длине волны D=lm, m= ±1, ± 2, ±3…
Это фактически означает, что лучу, проходящему через любую точку щели, можно поставить в соответствии отстоящий от него на b/2 и имеющий разность хода, равную нечетному числу полуволн. Приходя в точку наблюдения в противофазе, такие пары лучей гасят друг друга, образуя дифракционный минимум.
При наклонном падении разность хода крайних лучей, как видно из рисунка,
D= b sin(j)-b sin(q).
Тогда направления на первые фраунгоферовы минимумы (m= ±1) имеет место в соответствии с условием b (sin(j)- sin(q))=±l.
Откуда sin(j) = ± 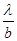 + sin(q).
+ sin(q).
И j = arcsin(± 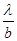 + sin(q)).
+ sin(q)).
Расчеты дают: j+1 = 330; j-1 = 270
Ответ: j = arcsin(± 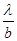 + sin(q)); j+1 = 330; j-1 = 270.
+ sin(q)); j+1 = 330; j-1 = 270.
Задача 3./Г.23.10/
Период дифракционной решетки d =5× 10-4 см. какой элемент дифракционной картины будет наблюдаться под углом j = p/6, если решетку освещать монохроматическим светом с длиной волны l= 600 нм, а ширина решетки l =0, 25 см.
Дано: Решение:
d =5× 10-4 см Структура (элементы) дифракционной картины,
j = p/6 получаемой с помощью дифракционной решетки.
l= 600 нм Решение задачи можно проводить путем последовательной
l =0, 25 см проверки выполнимости указанных условий главных и
добавочных максимумов и минимумов.
Условие главных максимумов: d sin(j)= ml,
отсюда 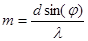 , m =
, m = 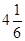 .
.
Полученный номер элемента имеет не целочисленное значение, а значит наблюдается не главный максимум, а элемент картины, расположенный между 4 и 5 главными максимумами.
Условие добавочных минимумов d sin(j)= 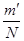 l.
l.
Число щелей N = l / d.
То есть условие принимает вид d sin(j)= 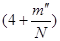 l,
l,
Откуда 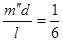 и m ¢ ¢ =
и m ¢ ¢ = 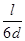 = 83
= 83 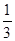 .
.
m ¢ ¢ тоже не целочисленное, т.е. наблюдается элемент картины между 83 и 84, лежащими между 4 и 5 главными максимумами.
Если считать приближенно, что добавочному максимуму между этими минимумами соответствует и m ¢ ¢ = 83 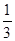 , то элементом дифракционной картины будет рост интенсивностив добавочном максимуме, расположенном между 83 и 84 добавочными минимумами, лежащими за 4 главным максимумом.
, то элементом дифракционной картины будет рост интенсивностив добавочном максимуме, расположенном между 83 и 84 добавочными минимумами, лежащими за 4 главным максимумом.
Задача 4. /Ир 5.145/
Свет, содержащий две спектральные линии с длинами волн 600, 000 и 600, 050 нм, падает нормально на дифракционную решетку ширины 10, 0мм. Под некоторым углом дифракции j эти линии на пределе разрешения (по критерию Рэлея). Найти угол j.
Дано: Решение:
l1=600.000 нм Согласно определению разрешающей силы и
l2= 600, 050 нм разрешающей силе дифракционной решетки
l = 10, 0 мм имеем
j -? 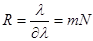 .
.
Условие главных максимумов решетки:
d sin(j)= ml,
Умножим его слева и справа на число щелей решетки:
N d sin(j)= N ml.
Произведение N d есть длина решетки l=Nd, а произведение N m есть способность 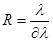 .
.
Тогда l sin (j)= 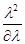 или sin(j)=
или sin(j)= 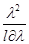 .
.
С учетом близости длин волн имеем dl = l2- l1, l2» l1 l2» l12.
Тогда j= 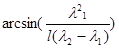 .
.
j = 460
Ответ: j= 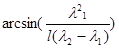 , j = 460
, j = 460