Методы определения порядка реакции. Исходные данные для определения порядка реакции обычно берутся из экспериментально определенных кинетических кривых

Исходные данные для определения порядка реакции обычно берутся из экспериментально определенных кинетических кривых. При этом во всех методах может быть определен либо временной порядок (одна кинетическая кривая), либо концентрационный (несколько кинетических кривых, а концентрации и скорости берутся только для нулевого момента времени).

Если в реакции участвует несколько исходных веществ, то, как правило, невозможно определить одновременно все частные порядки. Их значения определяются последовательно для каждого реагента. Для этого используется процедура, известная как «метод изолирования Оствальда». Суть ее состоит в том, что концентрации всех реагентов кроме одного берутся в большом избытке. Тогда в ходе кинетического эксперимента концентрации этих веществ могут считаться примерно постоянными и эффективный (или концентрационный) порядок по этим веществам будет равен нулю. В этом случае кинетическое уравнение упрощается. Например, из уравнения будет получено уравнение. Для определения величины 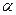в уравнении может быть применен один из трех следующих наиболее типичных методов.

1.5.1. Метод подстановки (метод проб и ошибок). Этот метод уже был описан ранее, он заключается в подстановке экспериментальных данных в уравнения, и для расчета константы скорости. Если порядок выбран правильно, то значения константы для различных моментов времени (или различных начальных концентраций при определении концентрационного порядка) должны быть приблизительно постоянны. В графической разновидности этого метода строятся графики в координатах - 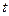(см. рис. 2). Линейная зависимость на графике указывает на правильно выбранный порядок. Недостаток метода – трудоемкость, субъективность полученного вывода и неприменимость метода в случае дробного порядка.

1.5.2. Метод определения порядка по времени полупревращения (метод Раковского). Если прологарифмировать уравнение, то получим:

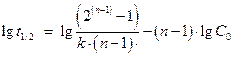
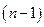Это уравнение представляет линейную зависимость в координатах . Угловой коэффициент этой зависимости равен , где 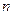- искомый порядок реакции. Ограничения метода: 1) метод применим только при достаточно полном протекании реакции (то есть когда начальная концентрация реагента изменяется не менее чем в два раза); 2) уравнения и, а значит и этот метод, неприменимы при 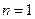. Если 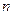имеет дробное значение и численно близко к единице, метод может давать слишком большую погрешность.

1.5.3. Дифференциальный метод Вант-Гоффа. Если прологарифмировать уравнение 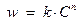, получим:

Построив график в координатах 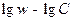, мы должны получить линейную зависимость, угловой коэффициент которой и равен порядку реакции. В отличие от двух предыдущих методов (относящихся к группе интегральных) в методе Вант-Гоффа для построения графика необходимы значения скорости при различных концентрациях. Скорость – это производная концентрации по времени. Эта величина может быть получена из кинетической кривой, как угловой коэффициент касательной в выбранной точке. Дифференциальный метод Вант-Гоффа привлекателен своей простотой и теоретически позволяет найти любое значение 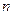. Однако необходимые пары данных «скорость – концентрация» экспериментально значительно труднее получить, чем пары значений «концентрация – время».