Основной закон кинетики.

Зависимость скорости химической реакции от концентрации С_i определяется основным законом кинетики согласно которому Скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, взятых в некоторых степенях.

Т. е. для реакции

аА + bВ + dD +... ––> еЕ +...

можно записать:

(3.5)

Коэффициент пропорциональности k есть константа скорости химической реакции. Константа скорости численно равна скорости реакции при концентрациях всех реагирующих веществ, равных 1 моль/л.

Зависимость скорости реакции от концентраций реагирующих веществ определяется экспериментально и называется кинетическим уравнением химической реакции. Очевидно, что для того, чтобы записать кинетическое уравнение, необходимо экспериментально определить величину константы скорости и показателей степени при концентрациях реагирующих веществ. Показатель степени при концентрации каждого из реагирующих веществ в кинетическом уравнении химической реакции (в уравнении (3.5) соответственно x, y и z) есть частный порядок реакции по данному компоненту. Сумма показателей степени в кинетическом уравнении химической реакции (x + y + z) представляет собой общий порядок реакции. Следует подчеркнуть, что порядок реакции определяется только из экспериментальных данных и не связан со стехиометрическими коэффициентами при реагентах в уравнении реакции.

Для того чтобы найти общий порядок реакции, достаточно в эксперименте исходные вещества (реагенты) взять в стехиометрическом соотношении. Порядок реакции по данному реагенту можно определить, взяв все остальные реагенты в таком избытке, что их изменением можно пренебречь.

При этом общий порядок реакции по данному реагенту можно рассчитать, используя:

а) метод, основанный на зависимости начальной скорости реакции от исходной концентрации реагентов;

б) метод, основанный на зависимости изменяющейся во времени скорости реакции от концентрации реагента.

Рассмотрим эти два метода на примере реакции

А + В → С + D

При использовании первого метода проводят серию опытов с различными исходными концентрациями реагента А (С_{А, 0}), снимая зависимость С_А(τ).

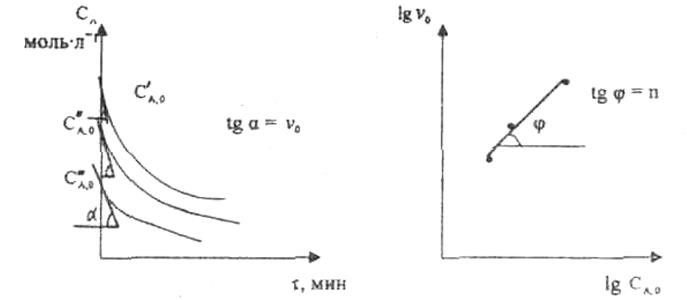
Рис. 3.4 Рис. 3.5

Для каждого опыта определяют известными методами начальную скорость реакции и по уравнению

, (3.6)

графическим или аналитическим методом определяют порядок реакции.

порядок реакции равен тангенсу угла наклона прямой к оси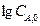

При применении второго метода в начале определяют в различные моменты времени концентрацию реагента А(С_А). Затем строят график зависимости С_А(τ), по которому для различных моментов времени находят скорости реакции.

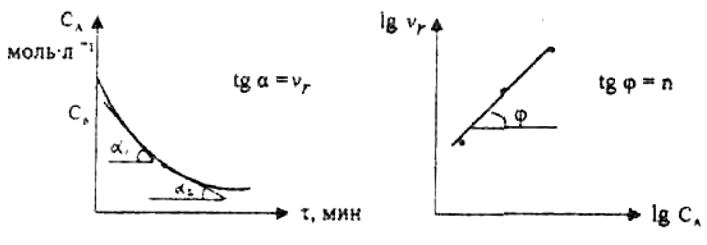
Рис. 3.6 Рис. 3.7

После этого используя известное уравнение

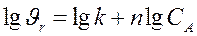, (3.7)

графическим или аналитическим методом определяют порядок реакции.

порядок реакции равен тангенсу угла наклона прямой к оси .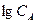

графическим или аналитическим методом определяют порядок реакции.

3.2. Зависимость скорости реакции от температуры.

Скорость химической реакции обычно растет с повышением температуры.Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:

При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.

Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ. Математически правило Вант-Гоффа можно записать следующим образом:

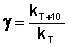(3.8)

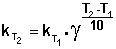(3.9)

Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).

Уравнение Аррениуса

Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.

Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.

Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции.

Рассмотрим термодинамический вывод выражения, описывающего зависимость константы скорости реакции от температуры и величины энергии активации – уравнения Аррениуса. Согласно уравнению изобары Вант-Гоффа,

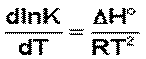(3.10)

Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (3.10) следующим образом:

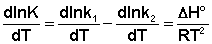(3.11)

Представив изменение энтальпии реакции Δ Hº в виде разности двух величин E₁ и E₂, получаем:

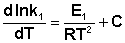(3.12)

(3.13)

Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где E_A – энергия активации:

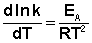(3.14)

После неопределенного интегрирования выражения (3.14) получим уравнение Аррениуса в интегральной форме:

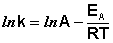(3.15)

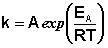(3.16)

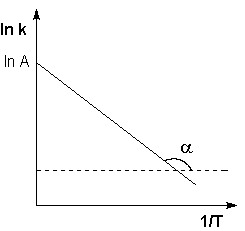
Рис. 3.8 Зависимость логарифма константы скорости химической реакции от обратной температуры.

Здесь A – постоянная интегрирования. Из уравнения (3.16) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (3.14), логарифм константы скорости линейно зависит от обратной температуры (рис.3.8); величину энергии активации E_A и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).

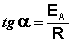(3.17)

Зная энергию активации реакции и константу скорости при какой-либо температуре T₁, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T₂:

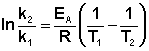(3.18)