Графическое интегрирование Проверка кинетического уравнения

кинетического уравнения интегральным методом

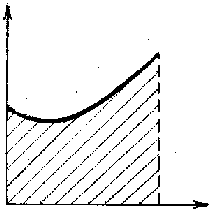
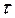
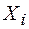
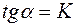
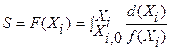
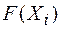
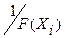
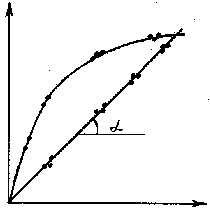
Рис. 3.9 Рис. 3.10

5) если экспериментальные точки не ложатся на прямую, необходимо испытать другие уравнения, пока не будет получено удовлетворительное соответствие.

Интегральный метод удобен для анализа простых кинетических уравнений, описывающих элементарные реакции.

Дифференциальный метод заключается в непосредственной проверке дифференциальной формы кинетического уравнения. Программу экспериментов в этом случае надо планировать так, чтобы сразу получить полную форму кинетического уравнения:

1) на основе предполагаемого механизма реакции получают кинетическое уравнение

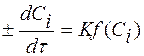(3.22)

2) по экспериментальной кривой изменения концентрации реагирующих веществ в координатах 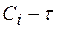графическим дифферен-цированием находят значения 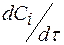в различные моменты времени и соответствующие этой скорости (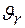) концентрации реагирующих веществ ();

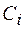3) составляют таблицу значений концентраций исходных реагирующих веществ и производной 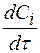через определённые интервалы времени. Используя эту таблицу, вычисляют значения функции ;

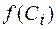4) строят график зависимости 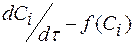. Если получают прямую линию, проходящую через начало координат, то это значит, что уравнение скорости соответствует экспериментальным данным (рис. 3.11);

Проверка кинетического уравнения дифференциальным методом

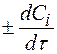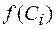
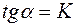
рис. 3.11

5) если график в координатах 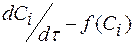не является прямой, то следует рассмотреть другое уравнение кинетики.