
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет медианы интервального ряда.
|
|
Если варианты в ряду распределения заданы в виде интервалов, то первоначально находят медианный интервал, который содержит единицу, находящуюся в середине ранжированного ряда. Для определения этого интервала сумму частот делят пополам и на основе последовательного суммирования частот первого, второго, третьего и т. д. интервалов находят интервал, где расположена медиана. Приближенное значение Ме в медианном интервале исчисляется по формуле:
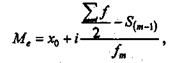
где хо — нижняя граница медианного интервала;
i — величина медианного интервала;
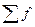 — сумма частот интервального ряда;
— сумма частот интервального ряда;
S(m-1) — сумма накопленных частот в интервалах предшествующих медианному;
fт — частота медианного интервала.
Из этой формулы следует, что к нижней границе медианного интервала (хо) добавляется та часть медианного интервала, которая пропорциональна удельному весу в частоте медианного интервала части ее, расположенной от нижней границы интервала до Ме.
Пример. В интервальном ряду (табл. 9) даны группы семей по среднемесячному доходу на 1 человека. Требуется определить для этого ряда серединное значение, т. е. медиану. Таблица.9