
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математична обробка результатів досліджень. Факторний експеримент
|
|
1 Статистичні методи обробки результатів експериментальних досліджень. Похибки. Розрахунки середніх значень та середньоквадратичних похибок. Методи вилучення грубих похибок. Послідовність математичної обробки експериментальних даних.
2 Застосування статистичних критеріїв для оцінки вірогідності отриманих експериментальних даних. Роль математичних методів планування багатофакторних експериментів у розв’язанні наукових проблем галузі.
1. При проведенні експерименту на кожний результат впливають всі можливі випадкові чинники, що не враховуються, тому всі реальні результати вимірювання є випадковими величинами, які відхиляються від істотного значення. Це відхилення називають похибкою спостереження.
Розрізняють три типи похибок:
- систематичні;
- випадкові;
- грубі.
Систематична похибка залишається постійною або закономірно змінюється при визначеннях однієї і тієї ж самої величини, що повторюється. Ці похибки є наслідком недосконалих приладів, неточності методу вимірювання, недогляду експериментатора, використання неточних даних при обчисленнях.
Випадкова похибка змінюється випадковим чином при вимірюваннях однієї і тієї ж самої величини, що повторюється. Вона може бути як позитивною, так і негативною, та викликатися суб’єктивними і об’єктивними причинами.
Груба похибка (промахи) – результат вимірювань якої-небудь величини, яка дуже відрізняється від інших результатів тієї ж серії.
Задача математичної обробки експериментальних даних полягає у виявленні і виключенні грубих, обліку систематичних і оцінці випадкових помилок.
Найбільш близьким до істинного значення величини, яку вимірюємо є середньоарифметичне
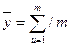
де m – кількість вимірювань;
u – номер досліду.
Абсолютна похибка u-го значення величини, яку вимірюємо:
∆ yu=yu-ӯ
Кількісною характеристикою розкиду результатів вимірювань yu навколо істинного значення ӯ є дисперсія випадкової величини σ 2. Однак, щоб одиниці у та σ були однакові, зручніше користуватися середньоквадратичним відхиленням 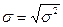
Оскільки істинне значення невідоме, користуються значенням ӯ, а замість дисперсії σ 2 – вибірковою дисперсією S2у, яка обчислюється по кінцевому числі вимірювань.
Інтервал (ӯ -ε; (ӯ +ε), в якому знаходиться із заданою імовірністю р істинне значення у, називається довірчим, величина ε – довірчою похибкою, а саме значення імовірності – довірчою вірогідністю р, або надійністю.
Величину 1- р - q називають рівнем значущості.
Існує декілька методів виключення грубих похибок дослідів, найбільш простим і швидким з яких є метод, оснований на оцінці максимальних розбіжностей результатів дослідів у.
Результати m дослідів розташовують в ряд по зростанню
y1, y2, y3……., ym-1, ym
Якщо «сумнівний» результат у1, то розраховують відношення
α =(у2-у1)/(уm-у1),
а якщо уm, то
α =(уm-уm-1)/(уm-у1),
При α > α кр «сумнівний» результат у1 є грубою похибкою і виключається з подальшої обробки.
Якщо ж «сумнівними» виявляться два найменших у1 та у2 або найбільших уm-1 та уm результати, то перевіряють це одним прийомом. Для цього обчислюють відношення
α =(у3-у1)/(уm-у1), або α =(уm-уm-1)/(уm-у1).
Якщо α > α кр, то обидва результати (у1, у2 або уm-1 та уm) є грубими похибками і повинні бути виключені з подальшої обробки.
Критичне значення α кр знаходять з таблиць, складених для різних значень q в залежності від кількості дослідів m і кількості результатів, що перевіряються (* - одного, ** - двох)
α кр[ q, m, * (або **) ].
Величину q звичайно приймають такою, що дорівнює 5 %.
Виключення грубих похибок за критерієм Стьюдента. Не використовуючи «сумнівний» результат ус, за формулами розраховують ӯ і S2yu, а потім обчислюють критерій Стьюдента (t-критерій)
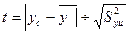 ,
,
Якщо t> tкр, то «сумнівний» результат ус є грубою похибкою.
Критичне значення критерію Стьюдента tкрзнаходять з таблиць, складених для різних значень q в залежності від числа ступенів вільності ƒ =m-1
tкр=(q, ƒ)
Виключення грубих похибок за критерієм максимального відхилення. Якщо за всіма m результатами дослідів визначено ӯ і S2yu, а потім виникла необхідність перевірки «сумнівного» результату ус, що вже ввійшов в їх розрахунок, то зробити це можна за критерієм максимального відхилення

Якщо r> rкр, то «сумнівний» результат ус є грубою похибкою і повинен бути виключений з подальшої обробки. Критичне значення критерію максимального відхилення rкр знаходять за таблицею в залежності від числа ступенів вільності ƒ =m-2:
rкр=(q, ƒ).
Абсолютні значення похибок не завжди достатні для характеристики точності проведених визначень, тому вдаються до визначення відносних похибок.
Відносні похибки одиничного або середнього результату обчислюють за формулами
δ уu=ε yu/yu, δ ӯ =ε ӯ /ӯ, (6.18)
де ε yu, ε ӯ - довірча похибка одиничного yu і середнього ӯ результатів.
Відносні похибки можна виразити у відсотках, помноживши результат обчислень за формулами (6.18) на 100 %.
Довірча похибка (граничне абсолютне відхилення) розраховується за допомогою критерію Стьюдента за формулами
ε yu=tкрSyu, ε ӯ =tкрSӯ ,
де Syu, Sӯ - середньоквадратичне відхилення одиничного і середнього результатів.
Величина tкр береться з таблиць в залежності від прийнятого рівня значущості q і числа ступенів вільності ƒ, що використовувався при визначенні дисперсії S2yu.
Потрібно зазначити, що величини
∆ yu=Syu/yu, ∆ y=Sӯ /ӯ
Виражені у відносних одиницях або у відсотках, називають відносним стандартним (середньоквадратичним) відхиленням.
Використовуючи величину довірчої похибки, можна визначити довірчий інтервал, в якому з наперед заданою довірчою вірогідністю р повинно лежати істинне значення величини, що вимірюється.
yu- ε yu< yu≤ yu+ ε yu,
ӯ -ε ӯ < ӯ ≤ ӯ + ε ӯ
Якщо величина δ ӯ досить велика, то для її зменшення збільшують кількість повторностей дослідів, після чого знову проводять обробку у вказаній вище послідовності.
Математичну обробку результатів дослідів рекомендовано проводити за наступною схемою:
1) перевірити наявність грубих похибок та їх виключення з подальшої обробки;
2) визначити середнє значення ӯ;
3) розрахувати дисперсії одиничного S2yu і середнього S2ӯ результатів;
4) визначити середньоквадратичні відхилення одиничного і середнього результатів Syu і середнього Sӯ ;
5) знайти довірчу похибку середнього результату ε ӯ ;
6) встановити довірчий інтервал, у якому з довірчою вірогідністю р буде знаходитись середнє значення ӯ;
7) визначити відносну похибку середнього результату δ ӯ .
Однорідність двох дисперсій перевіряють за критерієм Фішера (F-критерією), який дорівнює:
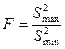
де S2max, S2min– більша та найменша з двох дисперсій.
Якщо розрахункове значення критерію Фішера менше критичного F< Fкр(q, ƒ 1 ƒ 2), тоді порівняльні дисперсії однорідні.
Де q – рівень значущості;
ƒ 1 – число ступенів вільності чисельника;
ƒ 2 – число ступенів вільності знаменника.
Якщо кількість порівняльних дисперсій більше двох, то їх однорідність перевіряють за критерієм Кохрена (G-критерію).
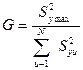
де N– число порівняльних дисперсій;
Кількість дослідів у кожній серії повинно бути однаковим, тобто m=const.
Якщо розрахункове значення критерію Кохрена G менше критичного, тоді дисперсії однорідні: G< Gкр, яке залежить від (q, N, ƒ).
де ƒ – число ступеня вільності максимальної дисперсії.
У технічних розрахунках величину довірчої вірогідності р звичайно приймають рівною 95 %, їй відповідає рівень значущості q, що дорівнює 5 %.
У більшості випадків експерименти багатофакторні. При проведенні багатофакторного експерименту використовуються класичний або факторний план. Класичний багатофакторний експеримент уявляє собою послідовність одно факторних експериментів, при яких всі незалежні змінні, крім однієї, приймаються постійними. У таких експериментах неможливе визначення характеру взаємодії факторів між собою та їх сумісного впливу на вихідний параметр.
Основою багатофакторного експерименту за факторним планом були розроблені Робертом Фішером у кінці 20-х років 20 століття. Багатофакторність експерименту дає можливість зміни його стратегії після чергового етапу. Багатофакторне планування дозволяє:
- отримати математичну модель процесу, яку використовують, наприклад, при керуванні;
- розкрити об’єктивні закономірності та отримати додаткову інформацію про процес;
- перевірити адекватність результатів експерименту.
Математична теорія експерименту та його планування, яка передбачає зміни усіх факторів, що досліджуються за визначеним планом та враховує їх взаємодію – це новий підхід до дослідження і використання ЕОМ для обробки результатів факторного експерименту.