
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача 1.Два параллельных бесконечно длинных проводника расположены на расстоянии 20 см
|
|
Задача 1. Два параллельных бесконечно длинных проводника расположены на расстоянии 20 см. Найти магнитную индукцию поля, создаваемого токами, протекающими по проводникам в противоположных направлениях (сила тока одинакова и равна 10 А), в точке А, равноудалённой от проводников на расстояние 40 см.
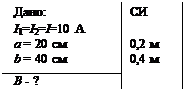 Решение.
Решение.
Физическая система состоит из двух проводников с током и создаваемого ими поля. Используем принцип суперпозиции для нахождения магнитной индукции
 (5.7)
(5.7)
где 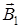 - магнитная индукция поля проводника с током I 1,
- магнитная индукция поля проводника с током I 1,
 – проводника с током I 2. Направления – проводника с током I 2. Направления  показаны на рис. 5.1. Ток, текущий от нас изображён крестиком, к нам – точкой. Модули В 1 и В 2 определим согласно (5.4): показаны на рис. 5.1. Ток, текущий от нас изображён крестиком, к нам – точкой. Модули В 1 и В 2 определим согласно (5.4):
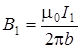 , ,
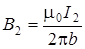 .
Так как по условию I 1 = I 2 = I, то .
Так как по условию I 1 = I 2 = I, то
| 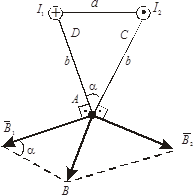 Рис. 5.1
Рис. 5.1
|
 . (5.8)
. (5.8)
По теореме косинусов 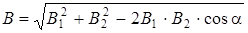
или с учётом (5.8):
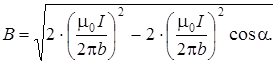 .(5.9)
.(5.9)
Найдём cosa по теореме косинусов, записанной для треугольника DCA:
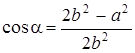 . (5.10)
. (5.10)
Подставим (5.10) в (5.9):
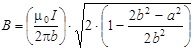
или
 .
.
Подставим числовые значения:
В 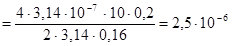 Тл =2, 5мкТл
Тл =2, 5мкТл
Ответ:  .
.
Задача 2. Два бесконечно длинных прямых провода скрещены под прямым углом. По проводам текут токи I1 = 1 A, I 2 = 2 A. Расстояние между проводами равно 10 см. Определить магнитную индукцию в точке А, удалённой от провода с током I 2 на расстояние 10 см. (см. рис. 5.2)
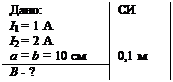 Решение.
Решение.
Магнитное поле в данной задаче создаётся двумя проводами с токами. Используем для нахождения магнитной индукции принцип суперпозиции:
 , (5.11)
, (5.11)
где 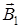 - магнитная индукция в точке А поля, создаваемого током I 1;
- магнитная индукция в точке А поля, создаваемого током I 1;  - магнитная индукция в точке А поля, создаваемого током I 2. Покажем на рис. 5.3 векторы
- магнитная индукция в точке А поля, создаваемого током I 2. Покажем на рис. 5.3 векторы 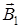 и
и  (вектор
(вектор  направлен от нас). Так как векторы перпендикулярны, модуль результирующего вектора определим по теореме Пифагора:
направлен от нас). Так как векторы перпендикулярны, модуль результирующего вектора определим по теореме Пифагора:
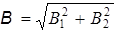 (5.12)
(5.12)
Значения В1 и В2 найдём в соответствии с (5.4):
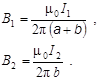 (5.13)
(5.13)
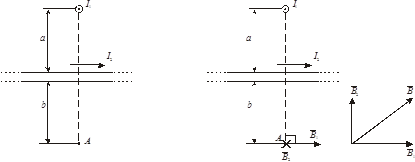
Рис. 5.2 Рис. 5.3
Подставим (5.13) в (5.12) и, с учётом a = b, получим:
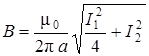
Подставляя числовые значения, получаем:
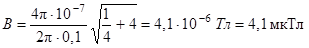 .
.
Ответ: 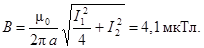
Задача 3. Используя принцип суперпозиции, найти магнитную индукцию поля в точке О, создаваемого дугой тонкого провода с током I = 10 А. Радиус дуги 10 см, дуга опирается на центральный угол p/3 радиан (рис. 5.4).
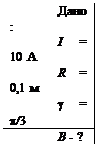 Решение.
Решение.
Физическую систему составляют дуга провода с током и магнитное поле этого тока. Разобьём дугу на элементарные участки длиной dl и рассмотрим один из них. Магнитная индукция поля, создаваемого таким элементарным участком, определяется законом (5.1):
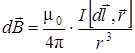
или для модуля dB:
 , (5.14)
, (5.14)
где a - угол между направлением тока на участке dl и направлением радиус-вектора, проведённого от dl к точке О, т.е. a = 90°. Направлен вектор  , в соответствии с правилом правого винта, для любого участка дуги от нас.
, в соответствии с правилом правого винта, для любого участка дуги от нас.
Магнитную индукцию поля, создаваемого всей дугой, находим по принципу суперпозиции:
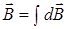
или 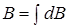 (5.15)
(5.15)
Подставим (5.14) в (5.15) и учтём, что sin 90° = 1,
 . (5.16)
. (5.16)
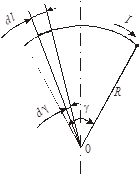 Рис. 5.4
Рис. 5.4
| Перейдём от dl к d g (см. рис. 5.4), чтобы упростить расчёт пределов интегрирования: dl = R d g.
Тогда (5.16) примет вид:
 (5.17)
Подставляя в выражение (5.17) угол g в радианах, мы можем найти магнитную индукцию в центре любой дуги.
Например, для окружности мы получим: (5.17)
Подставляя в выражение (5.17) угол g в радианах, мы можем найти магнитную индукцию в центре любой дуги.
Например, для окружности мы получим:
|
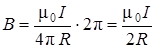 .
.
В нашем случае g = p/3, следовательно:
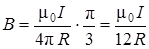 . (5.18)
. (5.18)
Легко заметить, что данная дуга представляет собой 1/6 часть окружности и магнитная индукция поля, создаваемого дугой, равна 1/6 магнитной индукции поля, создаваемого полной окружностью.
Подставим в (5.18) числовые значения и получим:
В» 10 –5 Тл = 10 мкТл.
Ответ: 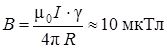 .
.
Задача 4. Бесконечно длинный провод изогнут так, как это показано на рис 5.5. Радиус дуги окружности R = 10 см. Определить магнитную индукцию в точке О, если по проводу протекает ток I = 20 А.
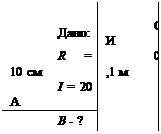
Решение.
Разобьём данный провод на три участка: I и III – прямолинейные, одним концом уходящие в бесконечность; II – дуга окружности (т.к. ей соответствует центральный угол в 120°, её длина равна трети окружности). Магнитную индукцию в точке О будем определять, используя принцип суперпозиции:
 ,
,
где 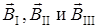 - магнитные индукции полей, создаваемых выделенными участками провода с током. Так как точка О лежит на оси провода I, то B I = 0 и, следовательно,
- магнитные индукции полей, создаваемых выделенными участками провода с током. Так как точка О лежит на оси провода I, то B I = 0 и, следовательно,
 .
.
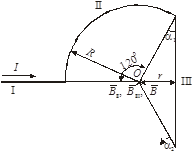 Рис. 5.5.
Рис. 5.5.
| Векторы 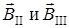 направлены в соответствии с правилом правого винта от нас, а значит результирующий вектор направлены в соответствии с правилом правого винта от нас, а значит результирующий вектор 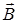 , тоже направлен от нас (см.рис. 5.5).
Модуль вектора В:
В = В II + B III. (5.19)
Величину В II найдём как треть от величины магнитной индукции в центре кругового тока (т.к. дуга равна трети окружности). , тоже направлен от нас (см.рис. 5.5).
Модуль вектора В:
В = В II + B III. (5.19)
Величину В II найдём как треть от величины магнитной индукции в центре кругового тока (т.к. дуга равна трети окружности).
|
В соответствии с (5.2) получим:
 . (5.20)
. (5.20)
Величину B III найдём согласно (5.5):
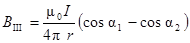 ,
,
где r = R× sin a1; a1 = 30°, a2 = 180° (см. рис. 5.5). Тогда:
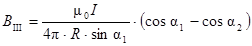 . (5.21)
. (5.21)
Подставим (5.20) и (5.21) в (5.19):
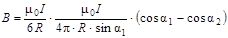 .
.
После подстановки числовых значений получим:
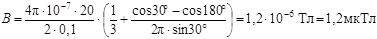
Ответ: В = 1, 2 мкТл.
Задача 5. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией В = 0, 3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.
Решение
Дано: Физическая система состоит из протона и
U = 600 В магнитного поля в котором он движется.
В = 0, 3 Тл  Движение заряженной частицы в одно-
Движение заряженной частицы в одно-
родном магнитном поле будет происходить по окружности
только в том случае, когда частица влетит в магнитное поле
R -? перпендикулярно линиям магнитной индукции 
 В.
В.
Т.к. сила Лоренца перпендикулярна вектору  , то она сообщит
, то она сообщит
частице (протону) нормальное ускорение ап.
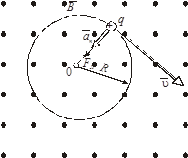
Рис. 6.1
Согласно второму закону Ньютона,
 , (6.5)
, (6.5)
где т – масса протона.
На рис. 6.1 совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора  . Силу Лоренца направим перпендикулярно вектору
. Силу Лоренца направим перпендикулярно вектору 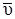 к центру окружности (векторы
к центру окружности (векторы  и
и 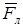 сонаправлены). Используя правило левой руки, определим направление магнитных силовых линий (направление вектора
сонаправлены). Используя правило левой руки, определим направление магнитных силовых линий (направление вектора  ).
).
Перепишем выражение (6.5) в скалярной форме (в проекции на радиус):
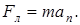 (6.6)
(6.6)
В скалярной форме 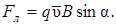 . В нашем случае
. В нашем случае 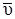
 В и sinα = 1, тогда
В и sinα = 1, тогда 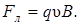 Так как нормальное ускорение ап =
Так как нормальное ускорение ап =  2/ R, то выражение (6.6) перепишем следующим образом:
2/ R, то выражение (6.6) перепишем следующим образом:
 .
.
Отсюда находим радиус окружности:
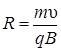 .
.
Заметив, что m  есть импульс протона (р), это выражение можно записать в виде
есть импульс протона (р), это выражение можно записать в виде
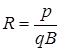 . (6.7)
. (6.7)
Импульс протона найдём, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. A = Δ Wk, или
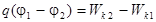 ,
,
где 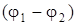 - ускоряющая разность потенциалов (или ускоряющее напряжение U);
- ускоряющая разность потенциалов (или ускоряющее напряжение U); 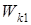 и
и 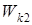 - начальная и конечная кинетические энергии протона.
- начальная и конечная кинетические энергии протона.
Пренебрегая начальной кинетической энергией протона (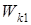
 0) и выразив кинетическую энергию
0) и выразив кинетическую энергию 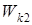 через импульс р, получим
через импульс р, получим
 .
.
Найдём из этого выражения импульс 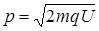 и подставим его в формулу (6.7):
и подставим его в формулу (6.7):
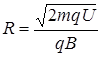 ,
,
или
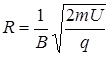 . (6.8)
. (6.8)
Подставим в формулу (6.8) числовые значения физических величин и произведём вычисления:
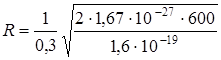 м = 0, 0118 м = 11, 8 мм.
м = 0, 0118 м = 11, 8 мм.
Ответ: 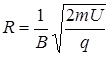 = 11, 8 мм.
= 11, 8 мм.
Задача 6. Электрон, влетев в однородное магнитное поле (В = 0, 2 Тл), стал двигаться по окружности радиуса R = 5 см. Определить магнитный момент рт эквивалентного кругового тока.
Решение 
Дано: Физическая система состоит из электрона и магнитного поля, в
В = 0, 2 Тл котором он движется. Электрон начинает двигаться по окружности,
R = 5 см если он влетает в однородное магнитное поле перпендикулярно
линиям магнитной индукции. На рис. 6.2 линии магнитной индук-
рт -? ции перпендикулярны плоскости чертежа и направлен «от нас»
(обозначены крестиками).
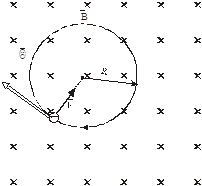
Рис. 6.2
Движение электрона по окружности эквивалентно круговому току, который в данном случае определяется выражением
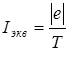 ,
,
где е – заряд электрона; Т – период его обращения.
Период обращения можно выразить через скорость электрона  и путь, проходимый электроном за период
и путь, проходимый электроном за период 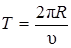 . Тогда
. Тогда
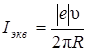 . (6.9)
. (6.9)
Зная Iэкв, найдём магнитный момент эквивалентного кругового тока. По определению, магнитный момент контура с током выражается соотношением
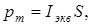 (6.10)
(6.10)
где S – площадь, ограниченная окружностью, описываемой электроном 
Подставив Iэкв из (1) в выражение (2), получим
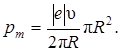
Сократим на π R и перепишем это выражение в виде:
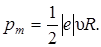 (6.11)
(6.11)
В полученном выражении известной является скорость электрона, которая связана с радиусом R окружности, по которой он движется, соотношением 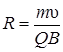 (см. пример 1). Заменив Q на | е |, найдём интересующую нас скорость
(см. пример 1). Заменив Q на | е |, найдём интересующую нас скорость  и подставим её в формулу (6.11):
и подставим её в формулу (6.11):
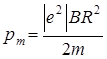 .
.
Произведём вычисления:
 А·м2 = 7, 03·10-12 А·м2 = 7, 03 пА·м2 .
А·м2 = 7, 03·10-12 А·м2 = 7, 03 пА·м2 .
Ответ: 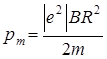 = 7, 03 пА·м2 .
= 7, 03 пА·м2 .
Задача 7. Электрон движется в однородном магнитном поле (В = 10 мТл) по винтовой линии, радиус R которой равен 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость  .
.
Решение
Дано: Физическая система состоит из электрона и магнитного поля.
В = 10 мТл  Электрон будет двигаться по винтовой линии, если он влетает
Электрон будет двигаться по винтовой линии, если он влетает
R = 1 см в однородное магнитное поле под некоторым углом (α = π /2)
h = 6 см к линиям магнитной индукции. Разложим, как это показано на
рис.6.3, скорость 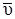 электрона на две
электрона на две
Т -? составляющие: параллельную вектору  ||)
||)
 -? и перпендикулярную ему (
-? и перпендикулярную ему (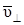 ).
).
Скорость 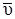 || в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль силовой линии. Скорость
|| в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль силовой линии. Скорость 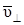 в результате действия силы Лоренца будет изменяться только по направлению (
в результате действия силы Лоренца будет изменяться только по направлению (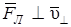 ); в отсутствие параллельной составляющей (
); в отсутствие параллельной составляющей (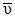 || = 0) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям).
|| = 0) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям).

Рис.6.3
Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении со скоростью  || и равномерном движении по окружности со скоростью
|| и равномерном движении по окружности со скоростью  . Период обращения электрона связан с перпендикулярной составляющей скорости соотношением
. Период обращения электрона связан с перпендикулярной составляющей скорости соотношением
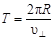 . (6.12)
. (6.12)
Найдём отношение 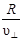 . Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение
. Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение 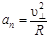 . Согласно второму закону Ньютона можно написать
. Согласно второму закону Ньютона можно написать
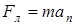 , или
, или 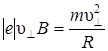 , (6.13)
, (6.13)
где 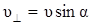 .
.
Сократив (6.13) на 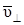 , выразим соотношение
, выразим соотношение 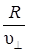 (
(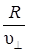 =
=  ) и подставим его в формулу (6.12):
) и подставим его в формулу (6.12):
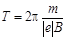 . (6.14)
. (6.14)
Произведём вычисления:
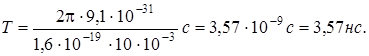
Модуль скорости  , как это видно из рис.6.3, можно выразить через
, как это видно из рис.6.3, можно выразить через  и
и  ||:
||:
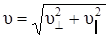 .
.
Из формулы (6.3) выразим перпендикулярную составляющую скорости:
 .
.
Параллельную составляющую скорости  || найдём из следующих соображений. За время, равное периоду обращения Т, электрон пройдёт вдоль силовой линии, т.е. h = T
|| найдём из следующих соображений. За время, равное периоду обращения Т, электрон пройдёт вдоль силовой линии, т.е. h = T  ||, откуда
||, откуда
 ||
||  .
.
Подставим вместо Т правую часть выражения (6.14), получим
 || =
|| = 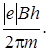
Таким образом, модуль скорости электрона
 =
= 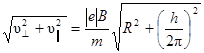 .
.
Произведём вычисления:
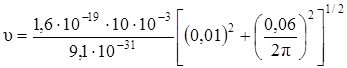 м/с =
м/с =  м/с, или 24, 6 Мм/с.
м/с, или 24, 6 Мм/с.
Ответ: 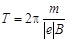 = 3, 57 нс;
= 3, 57 нс;  =
= 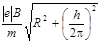 =
= 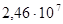 /с.
/с.
Задача 8. Альфа-частица прошла ускоряющую разность потенциалов U = 104 В и влетела в скрещенные под прямым углом электрическое (Е = 10 кВ/м) и магнитное (В = 0, 1 Тл) поля. Найти отношение заряда альфа-частицы к её массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.
 Дано: Решение.
Дано: Решение.
U = 104 В Физическая система состоит: α -частица, электрическое и
Е = 10 кВ/м магнитное поле.
В = 0, 1 Тл Для того, чтобы найти отношение заряда q альфа-частицы к
её массе т, воспользуемся связью между работой
сил электрического поля и изменением кинетической энергии частицы
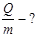
 ,
,
откуда 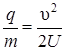 . (6.15)
. (6.15)
Скорость  альфа-частицы найдём из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:
альфа-частицы найдём из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:
а) сила Лоренца 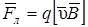 , направленная перпендикулярно скорости
, направленная перпендикулярно скорости 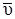 и вектору магнитной индукции
и вектору магнитной индукции  ;
;
б) кулоновская сила 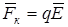 , сонаправленная с вектором напряженности
, сонаправленная с вектором напряженности 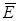 электростатического поля (q > 0). На рис. 6.4 направим вектор магнитной индукции
электростатического поля (q > 0). На рис. 6.4 направим вектор магнитной индукции  вдоль оси Oz, скорость
вдоль оси Oz, скорость 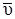 - в положительном направлении оси Ох, тогда
- в положительном направлении оси Ох, тогда 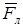 и
и 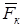 будут направлены так, как показано на рисунке.
будут направлены так, как показано на рисунке.
Альфа-частица не будет испытывать отклонения, если геометрическая сумма сил 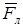 =
= 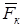 будет равна нулю. В проекции на ось Оy получим следующее равенство (при этом учтено, что
будет равна нулю. В проекции на ось Оy получим следующее равенство (при этом учтено, что 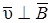 и sinα = 1):
и sinα = 1):
qE – q  B = 0,
B = 0,
откудa 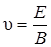 .
.
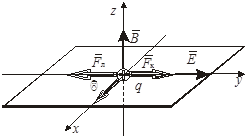
Рис. 6.4
Подставив это выражение скорости в формулу (6.15), получим
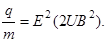
Произведём вычисления:
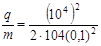 Кл/кг = 4, 81·107 Кл/кг = 48, 1 МКл/кг.
Кл/кг = 4, 81·107 Кл/кг = 48, 1 МКл/кг.
Ответ: 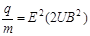 = 48, 1 МКл/кг.
= 48, 1 МКл/кг.
Задача 9. По двум параллельным прямым проводам длиной l =2, 5 м каждый, находящимся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу взаимодействия токов.
 Дано: Решение.
Дано: Решение.
l =2, 5 м Физическая система состоит: 2 провода с током и их магнит-
d = 20 см ные поля. Взаимодействие двух проводов, по которым текут
I = 1 кА токи, осуществляется через магнитное поле. Каждый ток создаёт магнитное поле, которое действует на другой провод
F -? Предположим, что оба тока (обозначим их для удобства I 1 и
I 2) текут в одном направлении. Ток I 1 создаёт в месте распо-
ложения второго провода (с током I 2) магнитное поле.
Проведём линию магнитной индукции (пунктир на рис.6.6) через второй провод и по касательной к ней – вектор магнитной индукции  . Модуль магнитной индукции В 1 определяется соотношением
. Модуль магнитной индукции В 1 определяется соотношением
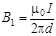 . (6.20)
. (6.20)
Согласно закону Ампера, на каждый элемент второго провода с током I 2 длиной dl действует в магнитном поле сила
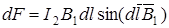 .
.
Так как вектор 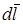 перпендикулярен вектору
перпендикулярен вектору  , то
, то 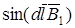 = 1 и тогда
= 1 и тогда
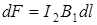 .
.
Подставив в это выражение В 1 согласно (6.19), получим
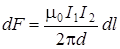 .
.
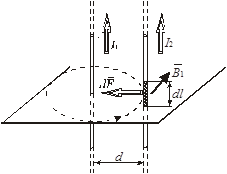
Рис. 6.6
Силу F взаимодействия проводов с током найдём интегрированием:
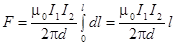 .
.
Заметив, что I 1 = I 2, получим
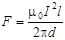 .
.
Произведём вычисления:
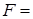
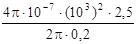 Н = 2, 5 Н.
Н = 2, 5 Н.
Сила  сонаправлена с силой
сонаправлена с силой 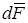 (рис.6.6) и определяется правилом правого винта.
(рис.6.6) и определяется правилом правого винта.
Ответ: 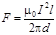 = 2, 5 Н.
= 2, 5 Н.