
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача1.Материальная точка массой 5 г осуществляет гармонические колебания с частотой 0,5 Гц
|
|
Задача1. Материальная точка массой 5 г осуществляет гармонические колебания с частотой 0, 5 Гц. Амплитуда колебаний равняется 3 см. Определить: 1) скорость точки в момент времени, если смещение точки от положения равновесия равняется 1, 5 см, 2) максимальную силу, которая действует на точку, 3) полную энергию колебаний.
Дано:
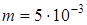 кг кг
 Гц Гц
 м м
 м м
| Решение.  А
х1
-А 0 А х
Рис.5.1.
А
х1
-А 0 А х
Рис.5.1.
|
| υ -? F max -? Е -? |
Рис.5.1.
1)Кинематическое уравнение гармонического колебания мате-ріальної точки вдоль оси x имеет вид:
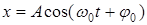 . (5.16)
. (5.16)
Чтобы найти скорость, продиференцем это уравнения за временем:
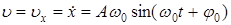 . (5.17)
. (5.17)
Чтобы выразить скорость через смещение, надо исключить из уравнений (5.16) и (5.17) время. Для этого подведем оба уравнения квадрат, разделим первое на A2, второе на A2 w2 и добавим:
. 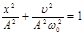
или с учетом (5.2):
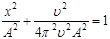
Отсюда:
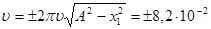 м/с.
м/с.
Знак плюс отвечает случаю, если направление скорости совпадает с направлением оси, знак минус - если направление скорости совпадает с отрицательным направлением оси x.
2)Силу, который действует на точку, найдем по второму закону Ньютона

, где а - ускорение точки, численное значение которого получим, продифференцировав скорость за временем (так как точка двигается по прямой, нормальное ускорение равняется нулю)
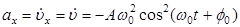
или

Зная ускорения, найдем силу:

отсюда максимальное значение силы:
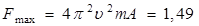 мН.
мН.
3) Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени. Вычислим полную энергию для момента времени, если кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равняется нулю. Итак,
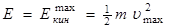 .
.
Из выражения (5.17) найдем:
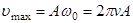 .
.
Итак,

Ответ: 1) 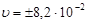 м/с, 2)
м/с, 2)  , 3)
, 3) 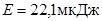 .
.
Задача 2. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями
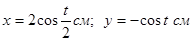
Найти уравнение траектории и построить её на чертеже.
Дано:
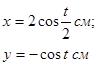
| Решение 1) В исходных данных уравнение траектории задано в параметрическом виде (т.е. как х(t); y = y(t)). Чтобы найти уравнение траектории в координатной |
| у = у(х) -? |
форме (т.е. как у = у(х)), необходимо исключить время t. Для этого воспользуемся тригонометрической формулой 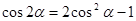 . В данном случае
. В данном случае 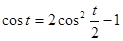 , т.е.
, т.е.
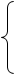
|
|
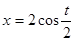
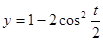
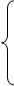
|
|
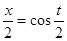


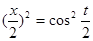 (1)
(1)
|

или вычитаем из уравнения (1) уравнение (2),
Рис.1 
Получилось уравнение параболы, вершина которого находится в т.С (0; 1), см. рис1.
 Задача 3. Физический маятник в виде тонкого прямого стержня длиной l = 120 см колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на некоторое расстояние а от центра масс стержня. При каком значении а период колебаний имеет наименьшее значение?
Задача 3. Физический маятник в виде тонкого прямого стержня длиной l = 120 см колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на некоторое расстояние а от центра масс стержня. При каком значении а период колебаний имеет наименьшее значение?
где J - момент инерции колеблющегося тела относительно оси колебаний (в данном случае т.О), Х – расстояние центра тяжести маятника от оси колебаний.
2) Момент инерции данного физического маятника (стержня) запишем с учетом теоремы Штейнера, как
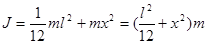
Тогда период колебаний запишется как
 (1)
(1)
3) Найдем экстремум функции Т = Т(х) (ф-ла 1). Для этого вычислим  :
:
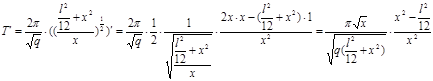 .
.
Решим уравнение  = 0, т.е.
= 0, т.е. 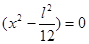
Отсюда 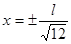 . Подходит
. Подходит 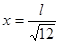 .
.
При х = 0, 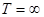 , а при
, а при 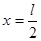 значение
значение 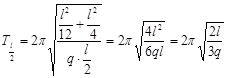 .
.
Если при 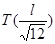 <
<  , то тем самым докажем, что при
, то тем самым докажем, что при 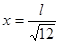 найдено
найдено 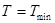 .
.  Вычислим
Вычислим 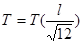 .
.
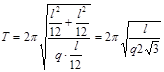 .
.
Тогда  < 1.
< 1.
 м.
м.
Ответ.
