Примеры решения задач. Задача 1. На диафрагму с круглым отверстием радиусом 1 мм нормально падает параллельный пучок света длиной волны l=0,5 мкм

Задача 1. На диафрагму с круглым отверстием радиусом 1 мм нормально падает параллельный пучок света длиной волны l=0, 5 мкм. На пути луча, что прошли через отверстие, помещают экран. Определить максимальное расстояние b_max от центра отверстия к экрану, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.

Дано:

r=1 мм=10^-3 м

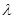=0, 5 мкм=5∙ 10^-7 м

b_max-?

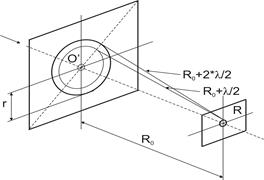
Рис. 4.1

Расстояние, при котором будет видно темное пятно, определяется числом зон Френеля, которые укладываются в отверстие. Если число зон четное, то в центре дифракционной картины будет темное пятно. Число зон Френеля, которые помещаются в отверстии, уменьшается по мере отдаления экрана от отверстия. Меньше четное число зон равняется двум. Итак, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, соответственно которого в отверстии должны поместиться две зоны Френеля.

Из рисунка 4.1 вытекает, что расстояние от точки наблюдения О на экране до края отверстия на 2∙ (l /2) большее, чем расстояние R₀= b_max. По теореме Пифагора получим:

r²=(b_max+2l/2)²- b_max²=2lb_max+ 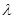²

Учтем, что l< < b_max и пренебрегая l² получим

r²=2lb_max

откуда

b_max= r²/2l =(10^-3)²/2∙ 5∙ 10^-7=1 м

Ответ: максимальное расстояние, при котором еще наблюдается темное пятно, равняется 1 м.

Задача 2. На расстоянии а=1 м перед диафрагмой с круглым отверстием радиусом R=1мм находится точечный источник света с длиной волны l=5∙ 10^-7 м. Отстань от диафрагмы к точке наблюдения b=2 м. Определить: 1) число зон Френеля в отверстии; 2) максимум или минимум интенсивности будет в центре дифракционной картины.

Дано:

R=1 мм=10^-3 м

а₁=1 м

l=5∙ 10^-7 м

b=2 м

k-?

Рис.4.2

Физическую систему составляет световая волна и диафрагма с круглым отверстием. Поскольку источник света находится на довольно близком расстоянии от диафрагмы, то световые волны будут сферическими, а явление, которое наблюдается на отверстии - дифракция Френеля.

Разобьем изображенную на рисунке 4.2 волновую поверхность Ф световой волны на зоны Френеля, что представляют собой сегменты радиусом r_k и высотой h_k. Из рисунка видно, что r_k можно выразить через два прямоугольных треугольника SCK, PCK:

r_k²=а²-(а-h_k)²

r_k²=b_k²-(b+h_k)²

где b_k - расстояниеот внешнего края k-ї зоны до точки Р

(b_k=b+k∙ l/2)

а²-а²+2аh_k- h_k²= b_k²-b ²-2bh_k-h_k²

2аh_k+2bh_k=b_k²-b

h_k=(b_k-b)/2(а+b)

учитывая то, что

b_k²=b²+klb+(k²l ²)/4=b²+klb

(k²l ²)/4 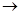0, получаем

h_k.=(klb)/2(а+b), тогда

r_k²=а²-(а-h_k)²=2аh_k-h_k² 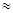2h_kа

h_k² 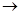0

r²=2аkl b/2(а+b)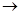

Поскольку радиус k - зоны Френеля совпадает с радиусом внешней k зоны Френеля r_k=R:

k=((а+b)R²)/аbl k =((1-2)∙ (10^-3)²)/1∙ 2∙ 5∙ 10^-7=3

Ответ: в отверстии укладываются три зоны Френеля, и так, в т. Р будет максимум дифракционной картины.

Задача 3. Посредине между точечным источником монохроматического света с длиной волны l=550 нм и экраном находится диафрагма с круглым отверстием. Дифракционная картина наблюдается на экране, расположенном на расстоянии 5 г от источника. Определить радиус отверстия, при котором центр дифракционных колец, которые наблюдаются на экране, будет наиболее темной.

Дано:

а= b=2, 5 м

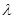=550 нм=5, 5∙ 10^-7 м

r-?

Пусть отверстие диафрагмы открывает k зон Френеля (см. рис. 4.2). Тогда радиус k-ї зоны Френеля есть не что другое, как радиус отверстия равный

r_k=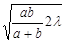

r_k= 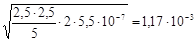м

Ответ: радиус отверстия в диафрагме 1, 17 мм.

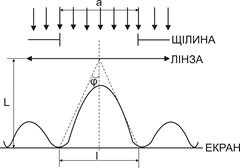
Задача 4. На щель шириной а=0, 1 мм падает нормально монохроматический свет с длиной волны l=500 нм. Дифракционная картина проектируется на экран, параллельный плоскости щели, с помощью линзы, расположенной вблизи щели. Определить расстояние от экрана к линзе, если отстань между двумя первыми дифракционными минимумами, расположенными по обе стороны от центрального максимума, равняется 1 см.

Дано;

а=0, 1 мм=10^-4 м

l=500 нм=5∙ 10^-7 м

l =1 см=10^-2 м

k=1

L-?

Рис. 4.3.

Условие дифракционных минимумов от одной щели, на которую падает нормально свет:

аsin j= k ,

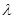где k=1 по условию задачи. Из рисунка 4.3 вытекает, что

l =2Ltgj,

но поскольку l /2< < L, то tgj 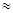sinj

sinj = l /2L

Подставляя значения sіnj в условие дифракционных минимумов от одной щели, получаем а l /2L=l

L=a l /2l

L=10^-4∙ 10^-2/2∙ 5∙ 10^-7=1 м

Ответ: расстояние от экрана к линзе равняется 1 м.

Задача 5. На дифракционную решетку нормально к ее поверхности падает монохроматический свет с длиной волны l=550 нм. На экран, который находится от решетки на расстоянии L=1м, с помощью линзы, расположенной вблизи решетки, проектируется дифракционная картина, причем первый главный максимум наблюдается на расстоянии l =12 см от центральных. Определить: 1) период дифракционной решетки; 2) число штрихов на 1 см ее длины; 3) максимальное число максимумов, который дает решетка; 4) угол дифракции, которая отвечает последнему максимуму.

Дано:

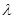=550 нм=5, 5 *10^-7 м

L=1 м

k=1

l =12 см=0, 12 м

l ’=1 см=0, 01 м

d-? n-? N-? j_max-?

Рис.4.4

Период дифракционной решетки найдем из условия главного максимума:

dsinj =k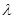

где k=1 - порядок спектра.

Из рисунка 4.4 вытекает, что tg j= l /L, так как l < < L, то

tg j 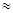sіnj и выражение можно записать:

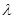
d l /L= d= lL/ l

Число штрихов на 1 см:

n= l ’/d=0.01/4.58∙ 10^-6=2.18∙ 10³ м^-1

Поскольку наибольший угол отклонения лучей решеткой не может быть более 90⁰ (p/2), тогда максимальное значение k_max можно найти из условия:

dsin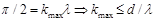

Естественно, что число k должно быть целым. Общее число максимумов, которое дает дифракционная решетка равняется:

N=2k_max+1

так как максимумы наблюдаются как по правую сторону так и по левую сторону от центрального максимума (единица учитывает центральный максимум):

N=(2d/l)+1=(2∙ 4.58∙ 10^-6/5.5∙ 10^-7)+1=17

Угол дифракции, которая отвечает последнему максимуму, найдем, записав условие максимумов от дифракционной решетки в виде:

dsin 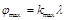откуда

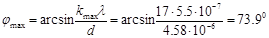
Ответ: период дифракционной решетки d=4, 58 мкм, число штрихов на 1 см длины решетки n=2, 18∙ 103 см^-1; максимальное число максимумов N=17; угол дифракции, которая отвечает последнему максимуму 73, 9⁰.

Задача 6. Дифракционная решетка длиной l =5 мм может различить в первом порядке две спектральных линии натрия l₁=589, 0 нм и l₂= 589, 6 нм. Определить, под каким углом в спектре третьего порядка будет наблюдаться свет с l₃=600 нм, что падает на решетки нормально.

Дано:

l =5 мм=5∙ 10³ м

l₁=589, 0 нм=5, 89∙ 10^-7 м

l₂=589, 6 нм=5, 896∙ 10^-7 м

l₃=600 нм=6∙ 10^-7 м

k₁=1

k₂=3

j-?

Для нахождения искомого угла запишем условие дифракционного максимума (см. рис.4.4):

dsinj =k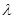_{3 3}

откуда

j =arcsin (k₃l ₃/ d) (1)

Период дифракционной решетки

d= l /N

где N - общее число штрихов дифракционных решеток.

Найдем N из формулы разрешающей способности дифракционных решеток,

R=k₁N=l ₁/Δ l

где

Δ l =l₂ - l ₁

тогда

N=l ₁/k₁Δ l

и

d= l k₁Δ l /l ₁ (2)

Подставив (2) в (1), найдем искомый угол:

j=arcsin(k₃l ₃l ₁/ k₁Δ l

j=arcsin(3∙ 6∙ 10^-7∙ 5.89∙ 10^-7/5∙ 10^-3∙ 1∙ 0.006∙ 10^-7)=20⁰42’

Ответ: свет в спектре третьего порядка будет наблюдаться под углом 20⁰42'.