Реальный колебательный контур.

Если колебательный контур содержит сопротивление, то возникают затухающие колебания. В уравнении, описывающем контур, появляется член, содержащий первую производную, поскольку мы должны учесть падение напряжения на сопротивлении. 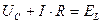. Используя выражения для тока и ЭДС самоиндукции, а также разделив все члены на L, получим: .

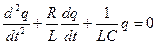Введем обозначение 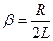. Как правило .

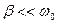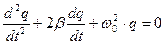
Представим решение в виде . Вычислим первую и вторую производные функции q(t) и подставим их в исходное уравнение: ;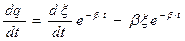

.

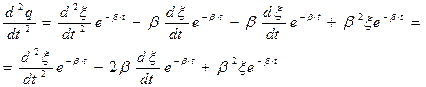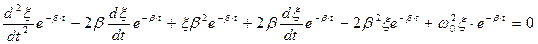
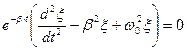
Легко видеть, что мы получили уравнение для функции 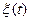, которое представляет собой уравнение гармонических колебаний с несколько иной частотой: 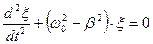Частота затухающих колебаний связана с собственной частотой .

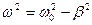Зависимость заряда на обкладке конденсатора от времени в этом случае .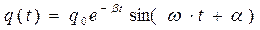

Зависимость величины тока от времени аналогична:

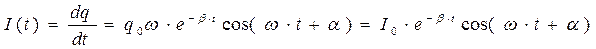
Слагаемым, содержащим в качестве сомножителя β, можно пренебречь.

Можно показать, что 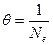, где число колебаний, в результате которых амплитуда уменьшается в е раз.

Добротность 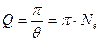. Энергия убывает со временем 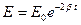(Здесь учтено, что энергия конденсатора пропорциональна квадрату напряжения, а энергия индуктивности – квадрату тока). Изменение энергии 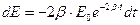. Потеря энергии, запасенной в контуре, за один период с хорошей точностью равна: 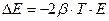. Относительное изменение энергии за один период .

.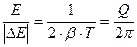
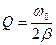
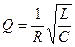