
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ток смещения.
|
|
Дело в том, что соотношение 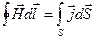 выполняется не всегда. Рассмотрим конденсатор и выберем контур вокруг участка с током. Если мы выберем поверхность, которая проходит между пластинами конденсатора, то никакой электронный ток её не пронизывает. Возникает парадокс. Чтобы спасти теорему о циркуляции, Максвелл предположил, что магнитное поле может создаваться не только реальным током, но должен существовать другой способ возникновения H. Другими словами, существует так называемый ток смещения.
выполняется не всегда. Рассмотрим конденсатор и выберем контур вокруг участка с током. Если мы выберем поверхность, которая проходит между пластинами конденсатора, то никакой электронный ток её не пронизывает. Возникает парадокс. Чтобы спасти теорему о циркуляции, Максвелл предположил, что магнитное поле может создаваться не только реальным током, но должен существовать другой способ возникновения H. Другими словами, существует так называемый ток смещения.
Представим себе плоский конденсатор, через который течет переменный ток.
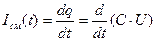 . Учитывая, что
. Учитывая, что 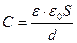 и
и 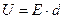 (это верно для однородного поля), получим:
(это верно для однородного поля), получим: 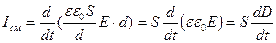 .
.
После добавления тока смещения уравнения Максвелла становятся более симметричными. Не только изменение магнитного поля приводит к появлению электрического, но и наоборот: изменение во времени электрического поля приводит к появлению магнитного!
Все известные явления электромагнетизма описываются уравнениями, которые получил Максвелл в 1864 г. В дифференциальной форме уравнения Максвелла имеют следующий вид:
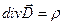 ;
;
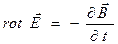 ;
;
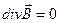 ;
;
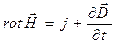 ;
;
Первое уравнение выражает теорему Гаусса в дифференциальной форме.
Второе уравнение описывает явление электромагнитной индукции.
Третье уравнение отражает тот факт, что не существует магнитных зарядов.
И, наконец, четвертое уравнение описывает появление магнитного поля как результат действия тока и включает в себя ток смещения.
Если ни электрическое поле, ни магнитное не зависят от времени, то уравнения “расщепляются”, первые два уравнения описывают электрическое поле, а вторые два уравнения – магнитное. Это означает, что электрическое поле не связано с магнитным.
В вакууме 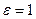 и
и 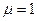 . Уравнения Максвелла принимают вид
. Уравнения Максвелла принимают вид
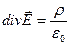 ;
; 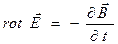 ;
; 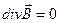 ;
; 
Из уравнений Максвелла следует, что даже в той области пространства, где нет токов (j = 0) и зарядов (ρ = 0), существует электромагнитное поле.
Вывод: вычисляем ротор от обеих частей второго уравнения: 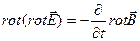
Пользуясь определениями, можно показать, что: 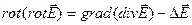 , где буквой Δ обозначен оператор Лапласа (лапласиан)
, где буквой Δ обозначен оператор Лапласа (лапласиан) 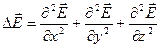 .
.
Так как ρ = 0 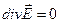 . Далее используем 4-е уравнение и получим
. Далее используем 4-е уравнение и получим
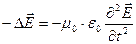
Окончательно получим волновое уравнение 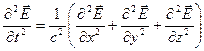 , где
, где 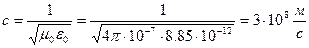 - скорость распространения волны.
- скорость распространения волны.
Аналогичное уравнение можно получить для магнитного поля.
Решение волнового уравнения  и
и 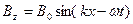 .
.
Таким образом, мы приходим к выводу, что даже в той области пространства, где нет заряженных частиц и токов, существует электромагнитная волна. Видимый свет – это электромагнитная волна. Однако, кроме видимого света, существуют электромагнитные волны, отличающиеся длиной волны – радиоволны, инфракрасное и ультрафиолетовое излучение, рентгеновские лучи и гамма-кванты.
В 1887-1888 гг. немецкий физик Г. Герц экспериментально доказал существование электромагнитных волн. Волны излучал диполь, состоящий из двух пластин, присоединенных к индукционной катушке и разделенных искровым промежутком. При проскакивании искры в системе возникали собственные колебания тока с частотой ν = 5108 Гц, диполь излучал волны с длиной 0.6 м. Герц регистрировал волны на некотором расстоянии от вибратора с помощью проволочного витка (резонатора).