
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ограниченные числовые множества. Точные грани числовых множеств
|
|
Лекция №4
Определение 1. Числовое множество 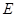 называется ограниченным сверху (снизу), если существует число
называется ограниченным сверху (снизу), если существует число 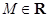 (
(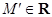 ) такое, что для всех
) такое, что для всех 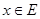 выполняется неравенство
выполняется неравенство 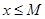 (
(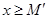 ).
).
Определение 2. Числовое множество, которое ограничено и сверху и снизу, называется ограниченным. Примерами ограниченных числовых множеств являются отрезок, интервал, полуоткрытый промежуток.
Число 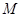 (
(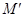 ) называется верхней (нижней) границей множества
) называется верхней (нижней) границей множества 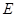 .
.
Определение 3. Наименьшая из верхних границ непустого ограниченного сверху множества 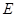 называется точной верхней гранью этого множества и обозначается
называется точной верхней гранью этого множества и обозначается 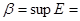
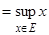 (supremum).
(supremum).
Теорема 1. Непустое множество, ограниченное сверху, имеет точную верхнюю грань, притом единственную.
Теорема 2. Для того чтобы число 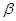 было точной верхней гранью непустого числового множества
было точной верхней гранью непустого числового множества 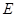 , необходимо и достаточно, чтобы:
, необходимо и достаточно, чтобы:
1) для всех 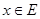 выполнялось неравенство
выполнялось неравенство 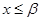 ;
;
2) для любого действительного числа 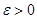 нашлось такое
нашлось такое 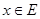 , что
, что 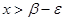 .
.
Определение 4. Наибольшая из нижних границ непустого ограниченного снизу множества 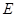 называется точной нижней гранью этого множества и обозначается
называется точной нижней гранью этого множества и обозначается 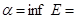
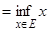 (infimum).
(infimum).
Теорема 3. Непустое множество, ограниченное снизу, имеет точную нижнюю грань, притом единственную.
Теорема 4. Для того чтобы число 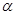 было точной нижней гранью непустого числового множества
было точной нижней гранью непустого числового множества 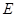 , необходимо и достаточно, чтобы:
, необходимо и достаточно, чтобы:
1) для всех 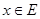 выполнялось неравенство
выполнялось неравенство 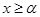 ;
;
2) для любого действительного числа 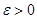 нашлось такое
нашлось такое 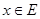 , что
, что  .
.
Пример 1. Пусть 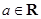 ,
, 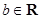 и
и 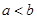 , тогда
, тогда
 и
и 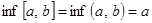 .
.
Этот пример показывает, в частности, что нижняя и верхняя грани могут как принадлежать, так и не принадлежать самому множеству.
Пример 2. Пусть 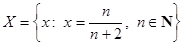 . Докажем, что
. Докажем, что 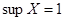 ,
, 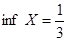 .
.
Решение. Для любого натурального числа 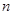 имеем
имеем 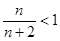 , а потому 1 – одна из верхних граней для
, а потому 1 – одна из верхних граней для 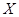 . Предположим теперь, что
. Предположим теперь, что 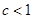 . Тогда найдется такое
. Тогда найдется такое 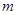 , что
, что 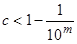 . С другой стороны,
. С другой стороны, 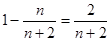 , а потому при
, а потому при 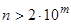 имеем
имеем 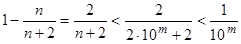 . Из этого неравенства следует, что
. Из этого неравенства следует, что 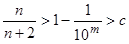 . Мы нашли, таким образом, элемент
. Мы нашли, таким образом, элемент 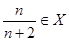 , такой, что
, такой, что 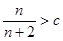 . Итак, для множества
. Итак, для множества 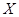 и числа 1 выполнены оба сформулированных выше утверждения, и потому
и числа 1 выполнены оба сформулированных выше утверждения, и потому 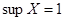 . Само число 1 не принадлежит
. Само число 1 не принадлежит 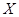 .
.
Далее, имеем 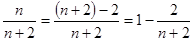 . Отсюда видно, что при увеличении
. Отсюда видно, что при увеличении 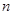 разность
разность 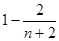 увеличивается. Значит, наименьшее значение разности достигается при
увеличивается. Значит, наименьшее значение разности достигается при 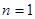 , и это значение равно
, и это значение равно 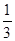 . Таким образом,
. Таким образом, 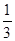 – наименьший элемент множества
– наименьший элемент множества 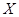 , а потому
, а потому 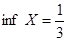 .
.