Лемма о вложенных отрезках

В математическом анализе при доказательстве многих важных утверждений аксиома полноты множества действительных чисел используется в виде принципа Коши-Кантора, называемого леммой о вложенных отрезках.

Определение 3. Система числовых отрезков

, , …, , …, , ,

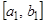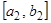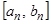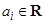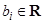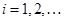
называется системой вложенных отрезков, если

,

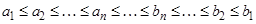т.е., если

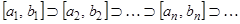(рис. 1).

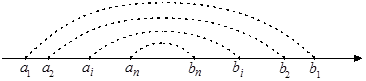Рис. 1

Лемма 1. Всякая система вложенных числовых отрезков имеет непустое пересечение.

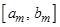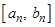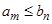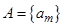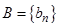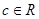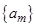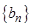Доказательство. Для любых двух отрезков и нашей последовательности имеет место , в противном случае отрезки бы не имели бы общих точек. Таким образом для числовых множеств и выполнены условия аксиомы полноты, в силу которой найдется число такое, что для любых и выполнено 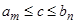. В частности, 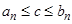для любого 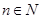. А это и означает, что точка с принадлежит всем отрезкам.

Лемма 2. Для всякой системы вложенных отрезков, длины которых стремятся к нулю, существует единственная точка 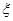, принадлежащая всем отрезкам данной системы.

Существование такой точки следует из теоремы 1. Докажем единственность. Предположим противное. Пусть 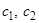– две точки, обладающие этим свойством. Если они различны и, например 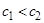, то при любо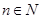м имеем 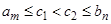, поэтому 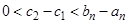и длина каждого отрезка нашей последовательности не может быть меньше положительной величины . Значит, если в последовательности есть отрезки сколь угодно малой длины, то общая точка у них единственная