
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лемма Бореля-Лебега
|
|
Лемма (Бореля-Лебега). Всякое открытое множество на числовой оси представляет собой сумму конечного или счетного числа попарно непересекающихся интервалов.
Теорема 1. Объединение конечного числа и пересечение произвольного числа замкнутых множеств есть замкнутое множество.
Теорема 2. Дополнение замкнутого множества есть множество открытое.
Теорема 3. Объединение произвольного числа и пересечение конечного числа открытых множеств есть открытое множество.
Перечислим также некоторые следствия, вытекающие из рассмотренных выше определений и утверждений.
1) Конечное множество не имеет предельных точек.
2) Каждое рациональное число является точкой прикосновения множества иррациональных чисел.
3) Каждое действительное число является точкой прикосновения множества рациональных чисел.
4) Пустое множество замкнуто и открыто одновременно.
5) Множество 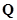 не открыто и не замкнуто в
не открыто и не замкнуто в 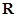 .
.
6) Множество 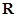 является как открытым, так и замкнутым.
является как открытым, так и замкнутым.
7) Любая 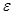 -окрестность точки
-окрестность точки 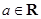 – открытое множество.
– открытое множество.
8) Отрезок 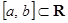 является замкнутым множеством.
является замкнутым множеством.