
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В ТАУ устойчивость – способность системы самостоятельно возвращаться в состояние равновесия после вывода ее из этого состояния и снятия всех возмущающих воздействий.
|
|
Анализ устойчивости линейных СУ
Всякая система управления должна быть работоспособной, т.е. нормально функционировать и быть не чувствительной к посторонним возмущениям различного вида. Работоспособность выявляется на основании одной из главных динамических характеристик системы – устойчивости.
Понятие устойчивости системы управления связано со способностью возвращаться в состояние равновесия после исчезновения внешних воздействий, которые вывели ее из этого состояния. Данное определение является физическим определением понятия устойчивости. Наглядно устойчивость равновесия иллюстрируется на рис.5.1. Здесь положение шарика определяется координатой y. Выведем шарик из положения равновесия в точку y0 и отпустим его.
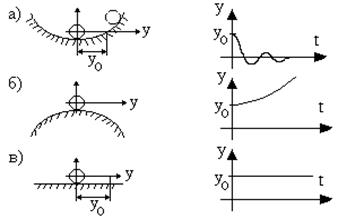
Рис. 5.1. Иллюстрация понятия устойчивости
Из анализа изменения координаты y(t) следует:
а) y(t)®0 при t®¥, устойчивое положение шарика;
б) y(t)®¥ при t®¥, неустойчивое положение шарика;
в) y(t)=y0=const при t³ 0, нейтральное или безразличное положение шарика.
В ТАУ устойчивость – способность системы самостоятельно возвращаться в состояние равновесия после вывода ее из этого состояния и снятия всех возмущающих воздействий.
Если система описывается линейными дифференциальными уравнениями, то ее устойчивость не зависит от величины и вида возмущения, а зависит только от знака вещественной части корней характеристического уравнения.
Характеристическое уравнение – это уравнение, полученное приравниванием знаменателя передаточной функции к нулю.
Согласно теории устойчивости Ляпунова – для устойчивости системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, или эти корни на плоскости комплексного переменного были расположены слева от мнимой оси (рис.5.5).
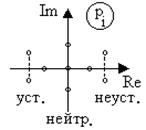
Рис. 5.5. Комплексная плоскость корней характеристического уравнения
Если корни характеристического уравнения расположены на мнимой оси, то система находится на границе устойчивости. При этом возможны два случая: корень в начале координат и пара мнимых корней. Нулевой корень появляется, когда свободный член характеристического уравнения равен нулю. В этом случае границу устойчивости называют апериодической. Если остальные корни этого уравнения имеют отрицательные вещественные части, то система устойчива не относительно выходного сигнала, а относительно его производной, выходной сигнал в установившемся режиме имеет произвольное значение. Такие системы называют нейтрально устойчивыми. В том случае, когда характеристическое уравнение имеет пару мнимых корней, границу устойчивости называют колебательной.
Если хотя бы один из корней лежит в правой полуплоскости комплексной плоскости корней характеристического уравнения, то система неустойчивая.
Корни полинома можно находить при помощи пакетов Mathcad и Matlab. Пусть исходный полином представлен в виде: f(x) = (x–3)(x–1)2 = x4 – 6x3 + 12x2 – 10x + 3. Пишем в Mathcad через пробел начиная со свободного члена v: = (3 –10 12 –6 1)T – это транспонированная матрица. Чтобы ее создать нажимаем сначала Insert Matrix, Rows – 1, Columns – 5. Вводим через пробел коэффициенты. После этого нажимаем кнопку MT. После этого пишем polyroots (v) =  если все ввели правильно, появится ответ в виде скобок с корнями в строках
если все ввели правильно, появится ответ в виде скобок с корнями в строках
Matlab Пусть исходный полином f(x) = x3 + 3x2 +4 Пишем по порядку через пробел p = [1 3 0 4]
r = roots(p)
r = 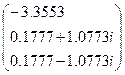
Определение знаков корней характеристического уравнения путем решения уравнений 4-го и более высоких порядков затруднительно, поэтому применяются косвенные методы анализа устойчивости или критерии устойчивости, которые позволяют определить знаки корней характеристического уравнения без решения этого уравнения.
Необходимым, но недостаточным условием устойчивости системы является положительность всех коэффициентов характеристического уравнения системы
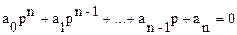 ,
,
т.е. соблюдение условия ai > 0 для всех i от 0 до n, где n - порядок системы.
Если хотя бы один их коэффициентов, кроме крайних, равен нулю, то САУ – неустойчива.