
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий устойчивости Михайлова
|
|
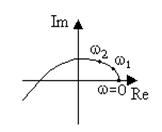
Для устойчивой системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси на число квадрантов, равное порядку характеристического уравнения, последовательно проходя эти квадранты.
На рис. приведены примеры годографов для устойчивой и неустойчивой систем.
а) б)
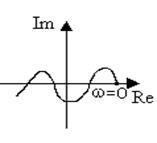
Рис. годограф Михайлова:
а - устойчивой системы 3-го порядка; б - неустойчивой системы
Если годограф проходит через начало координат, то система находится на границе устойчивости
Последовательность определения устойчивости:
– Х.У. переводится в частотную область путем подстановки вместо S значения 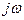
– разделяется вещественная и мнимая части Х.У.
– строится декартова система координат. Ось абсцисс – вещественная часть Х.У. Ось ординат - мнимая часть Х.У.
– в Х.У. переведенном в частотную область задаются значения 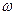 от нуля до бесконечности и вычислят отдельно вещественную и мнимую части этого уравнения
от нуля до бесконечности и вычислят отдельно вещественную и мнимую части этого уравнения
– полученные значения вещественной и мнимой части откладываются на декартовой системе координат в виде точек, которые соединяют плавной кривой и получают годограф Михайлова
– по виду прохождения годографа Михайлова судят об устойчивости данной системы.