
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка качества по частотным характеристикам.
|
|
Прямые методы оценки качества управления
Устойчивость САУ является необходимым, но не достаточным условием для ее эффективного функционирования. Важное значение имеет качество управления.
Качество СУ – обобщенная характеристика свойств системы, которая определяется поведением системы в установившихся и переходных режимах.
1. Точность системы
При оценке качества системы в установившихся режимах используют понятие точности системы. Точность системы характеризуется ошибками выходного сигнала. Ошибки могут возникать из-за неточного воспроизводства системой входного заданного сигнала или из-за действия возмущений.
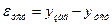
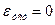 – астатическая система
– астатическая система
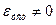 – статическая система
– статическая система
2. Показатели качества в переходном режиме
Для сравнения качества различных САУ исследуется их реакция на типовые воздействия. Обычно это единичная ступенчатая функция, как один из наиболее неблагоприятных видов возмущений. Для систем, работающих с периодическими возмущениями, целесообразно оценивать качество управления при гармоническом воздействии.
Все современные методы анализа качества управления можно разделить на прямые методы анализа по кривой переходного процесса или по частотным характеристикам, и косвенные методы, позволяющие, не решая дифференциального уравнения, определить некоторые показатели качества процесса управления; к ним, в частности, относятся корневые, интегральные и частотные методы.
Прямые показатели качества
Для определения таких показателей качества используют кривую переходного процесса, полученную при подаче на вход ступенчатого воздействия.
Качество систем управления в переходном режиме характеризуется следующими показателями:
1) временем переходного процесса (tПП). Теоретически переходной процесс может длиться бесконечно долго. tПП – интервал времени от начала переходного процесса до момента, когда отклонение управляемой величины от нового установившегося значения не будет превышать допустимых пределов


|
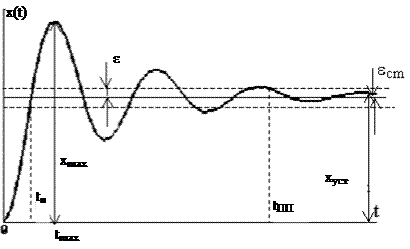 |
2) перерегулирование s представляет собой максимальное отклонение управляемой величины от нового установившегося значения и выраженное в процентах.
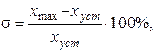
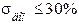
3) колебательность характеризуется числом колебаний управляемой величины за tПП (у нас 5)
nдоп ≤ 3
 4) характер затухания переходного процесса
4) характер затухания переходного процесса
а) апериодический
б) малоколебательный
в) колебательный
г) монотонный
5) время достижения первого максимума – время от момента начала переходного процесса до момента, когда выходная величина принимает максимальное значение tмах
6) время нарастания переходного процесса (tН) – минимальное время за которое переходная функция системы пересекает уровень установившегося значения
Достоинство прямых методов – наиболее достоверные данные
Недостатки:
1) Сложность вычисления для систем, описываемых дифф. уравнениями высоких порядков, особенно если требуется выяснить влияние отдельных параметров системы на показатели ее качества.
2) Прямые показатели неудобны, когда параметры системы не фиксированы и их трудно выбирать так, чтобы удовлетворить заданным требованиям ее качества.
Косвенные методы оценки качества
Они позволяют оценить качество системы без построения графика переходного процесса.
Достоинство: они позволяют судить о влиянии параметров системы на ее динамические свойства.
Существует несколько косвенных оценок, наиболее распространенными являются корневые методы, оценка по частотным характеристикам и интегральные оценки.
Метод распределения корней
Он основан на определении границ области расположения корней характеристического уравнения на комплексной плоскости и установлении связи переходного процесса с показателями указанных границ.
Достоинство: позволяет наглядно и достоверно просто оценить быстродействие системы и ее колебательность.
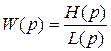
L(p) = 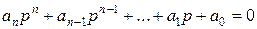 – характеристическое уравнение
– характеристическое уравнение
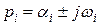 - i -тый корень характеристического уравнения
- i -тый корень характеристического уравнения
В соответствии с необходимым и достаточным условием устойчивости по Ляпунову необходимо, чтобы все корни характеристического уравнения имели отрицательную вещественную часть.
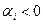
1) Расстояние α min = η от ближайшего корня до мнимой оси характеризует запас устойчивости системы и называется степенью устойчивости этой системы. Чем меньше значение α min, тем больше будет время переходного процесса

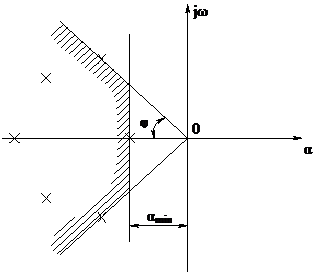
2) Наибольший из углов, образованных отрицательной вещественной полуосью и лучами, проведенными из начала координат через корни, характеризует колебательность системы cos φ = μ. Чем меньше значение μ, тем более система склонна к колебаниям. Для одновременного обеспечения заданного времени переходного процесса и заданной колебательности нужно, чтобы все корни характеристического уравнения лежали внутри заштрихованной области.
Оценка по частотным характеристикам
Идеальной системой считается система, которая в любой момент времени точно копирует входной сигнал (например, усилительное звено)
Для идеальной системы 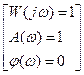
Для реальных систем из-за инерционности системы, которая отражается постоянными t ее звеньев 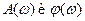 имеют следующий вид:
имеют следующий вид:


На участке 0< ω < ω 1 выполняются условия А(ω) ≈ 1 и 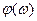 ≈ 0
≈ 0
На резонансной частоте (ω max) АЧХ имеет максимальное значение. При дальнейшем увеличении частоты, система вследствие своей инерционности не успевает реагировать на колебания больших частот и А(ω) резко падает, ФЧХ становится отрицательной, т.к. выходной сигнал отстает по фазе от входного. Т.о. система частотные характеристики которой представлены на рисунках может быть отнесена к классу фильтров нижних частот, которые хорошо пропускают колебания малых частот и плохо больших. 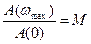 – коэффициент колебательности
– коэффициент колебательности
Чем больше М, тем более колебательным является переходной процесс. М=1, 2…1, 5
Малым значениям М соответствует большее время переходного процесса. При увеличении значения М, увеличивается перерегулирование и система приближается к границе устойчивости.
ω среза замкнутой СУ определяется тогда, когда амплитуда входных и выходных колебаний равны между собой 

ω п – полоса пропускания частот замкнутой системы. Чем меньше ω п, тем больший спектр входного сигнала передается системой без искажений и тем выше точность работы системы и больше быстродействие системы