
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условие оптимального распределения в системе с ТЭС
|
|
Рассмотрим энергосистему, в которой работает n ТЭС на одинаковом топливе. Известны расходные характеристики станций Bi(Pi). Задана суммарная нагрузка PH. Распределение проводят для каждой ступени суточного графика. При распределении без учета потерь в сети условия будут такими же, как и при распределении внутри ТЭС.
Получим условия оптимального распределения с учетом потерь в сети. Составим математическую модель. В качестве неизвестных приняты мощности ТЭС. Целевая функция определяет общий расход топлива
 ;
;
и ограничение по балансу мощности имеет вид: 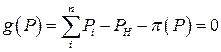 ,
,
где p - функция потерь мощности в сети.
Составим функцию Лагранжа:
 ;
;
и запишем условия минимума ее
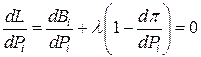 , i = 1, …, n;
, i = 1, …, n;
 ;
;
где 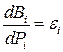 – удельный прирост расхода топлива на ТЭС.
– удельный прирост расхода топлива на ТЭС.
Откуда получаем условие
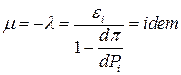
Выражение (3) при соблюдении баланса мощности является условием оптимального распределения.
Здесь частная производная  называется удельным приростом потерь. Он показывает, на сколько изменятся потери в сети при изменении нагрузки i-ой станции на 1 МВт при неизменных нагрузках остальных станций. Такое изменение определяется при выбранном балансирующем узле.
называется удельным приростом потерь. Он показывает, на сколько изменятся потери в сети при изменении нагрузки i-ой станции на 1 МВт при неизменных нагрузках остальных станций. Такое изменение определяется при выбранном балансирующем узле.
Обычно значение прироста потерь редко выходит за предел 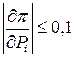 .
.
Рассмотрим смысл переменной m, учитывающей потери,
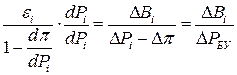
Таким образом, относительные приросты всех ТЭС по отношению к изменению мощности  должны быть одинаковы. Если в качестве балансирующего узла (БУ) взята n -я станция, то для нее
должны быть одинаковы. Если в качестве балансирующего узла (БУ) взята n -я станция, то для нее 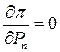 , тогда условия оптимальности выглядит несколько проще
, тогда условия оптимальности выглядит несколько проще
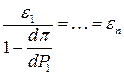 .
.