
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические основы работы. Изучение законов, по которым происходит колебательное движение математического и физического маятников
|
|
Лабораторная работа № 8
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ УНИВЕРСАЛЬНОГО МАЯТНИКА
ЦЕЛЬ РАБОТЫ
Изучение законов, по которым происходит колебательное движение математического и физического маятников, и экспериментальное определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Ускорение свободного падения (ускорение силы тяжести) - ускорение, которое приобретает свободная материальная точка под действием силы тяжести. Такое ускорение имел бы центр тяжести любого тела при падении тела на Землю с небольшой высоты в безвоздушном пространстве. Как и сила тяжести, ускорение свободного падения зависит от широты места и высоты его над уровнем моря [1].
Для установления физического смысла вектора ускорения силы тяжести (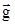 ) предположим, что внешние[1] силы отсутствуют и скорость материальной точки равна нулю. Тогда вектор
) предположим, что внешние[1] силы отсутствуют и скорость материальной точки равна нулю. Тогда вектор 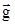 есть ускорение свободного падающего тела относительно Земли при условии, что скорость тела в данный момент времени равна нулю. Замечание по поводу равенства нулю скорости тела существенно, так как при наличии скорости u появляется дополнительное ускорение из-за кориолисовой силы.**
есть ускорение свободного падающего тела относительно Земли при условии, что скорость тела в данный момент времени равна нулю. Замечание по поводу равенства нулю скорости тела существенно, так как при наличии скорости u появляется дополнительное ускорение из-за кориолисовой силы.**
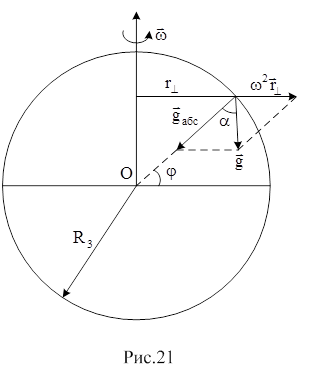
Таким образом, при указанных условиях ускорение свободного падения равно (рис.21):
 , (1)
, (1)
 где
где 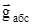 - ускорение, характеризующее гравитационное поле Земли и равное
- ускорение, характеризующее гравитационное поле Земли и равное
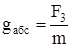 ,
,
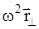 - ускорение, сообщаемое центробежной силой инерции и обусловленное суточным вращением Земли.
- ускорение, сообщаемое центробежной силой инерции и обусловленное суточным вращением Земли.
В каждой точке вектор определяется размерами, формой Земли и распределением вещества в ней. Вектор был бы точно направлен к центру Земли, если бы Земля была сферически - симметричной и вещество внутри нее было распределено равномерно. Направление отвеса (направление нити с грузом) определяется вектором, построенным на векторах и, т.е. различие между направлениями и для сферически - симметричной Земли обусловлено центробежной силой инерции, и направление к центру Земли не совпадает с направлением отвеса. Другой причиной различия направлений указанных векторов объясняется сплюснутость Земли вдоль оси суточного вращения (но это причина несущественно влияет на различие направлений и, ввиду малости сплюснутости и малой угловой скорости суточного вращения Земли). Сплюснутость Земли (и неравномерность распределения вещества) отражается на различии величины на полюсе и экваторе.
Если бы Земля была правильным шаром, то угол a между векторами 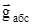 и
и 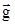 определялся бы формулой:
определялся бы формулой:
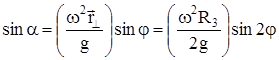 , (2)
, (2)
где j - географическая широта местонахождения точки,
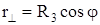 .
.
Следует отметить, что для реального земного шара формула (2) достаточно точна.
Проецируя векторы 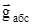 и
и 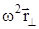 на направление вектора
на направление вектора 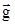 и учитывая, что a < < j и cosa» 1, получим формулу:
и учитывая, что a < < j и cosa» 1, получим формулу:
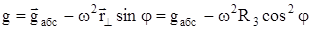 . (3)
. (3)
Величина ускорения свободного падения |g| может быть найдена экспериментально, что является целью данной лабораторной работы.
По данным [2] ускорение на полюсе gп = 983, 2 см/c2, на экваторе
gэ = 978, 0 см/c2 и по формуле (3) вычисляем значение gабс. На полюсе
gабс = gп = 983, 2 см/с2 (cosa = cos900 = 0) и на экваторе gабс = 981, 4 см/с2 (с учетом, что период суточного вращения Земли - звездные сутки T3 = 86164 c и
R3 = 6, 378× 106 м).
Считая, что Земля - правильный шар со сферически - симметричным распределением вещества в нем, можно показать, что ускорение свободного падения на Земной поверхности (на полюсе, где отсутствует центробежная сила, обусловленная суточным вращением Земли) определяется формулой:
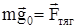 ,
,
 ,
,
отсюда  , (4)
, (4)
где G = 6, 67× 10-11 (Н× м2)/кг2 - гравитационная постоянная,
М3 = 5, 98× 1024 кг - масса Земли,
R3 = 6, 37× 106 - средний радиус Земли.
Можно показать, что ускорение силы тяжести на высоте h над Землей связано с ускорением g0 следующим соотношением:
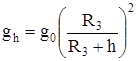 . (5)
. (5)
При определении ускорения свободного падения на глубине h следует иметь в виду, что тело испытывает притяжение не всей массой Земли, а только слоев, лежащих глубже этого тела.
В настоящее время существует ряд прямых и косвенных методов измерений ускорения силы тяжести.
Один из способов прямого измерения ускорения силы тяжести по времени падения шарика с известной высоты описан в [10]. Этот способ отличается простотой и наглядностью, но весьма неточен из-за ошибок, причинами возникновения которых являются неодновременность включения электрического секундомера и выключение электромагнита, удерживающего шарик в исходном состоянии, задержка между моментом падения шарика на пластину и разрывом цепи секундомера, что приводит к погрешности измерения времени падения шарика.
Большинство косвенных методов измерения ускорения силы тяжести основано на применении формул периода колебаний математического и физического маятников.
Прежде чем перейти к рассмотрению методики указанных способов измерения ускорения g, следует напомнить некоторые физические величины и законы (теоремы), которые будут полезны при выполнении данной лабораторной работы (для более детальной проработки нижеследующего материала можно воспользоваться литературными источниками [2, 3] и др.).
Важнейшие законы механики связаны с понятием момента силы (и момента импульса). Следует различать моменты этих векторов относительно неподвижного центра (точки) и относительно неподвижной оси. В данной лабораторной работе рассматривается только момент силы, поэтому целесообразно напомнить эту величину.
Момент силы относительно центра (точки) есть вектор. Момент силы относительно оси - это проекция на эту ось его момента относительно точки, лежащей на этой оси, т.е. момент силы относительно оси уже не является вектором.
Итак, момент силы 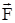 относительно центра О равен векторному произведению радиуса - вектора
относительно центра О равен векторному произведению радиуса - вектора 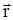 на силу
на силу 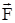 :
: 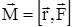 . (6)
. (6)
Вектор 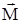 направлен перпендикулярно плоскости векторов
направлен перпендикулярно плоскости векторов 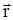 и
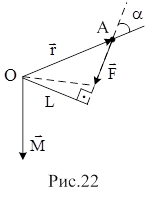
и 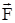 и образует с ними правовинтовую систему (рис.22).
и образует с ними правовинтовую систему (рис.22).
 Момент
Момент 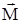 зависит от выбора центра О (или начала, или полюса). Точка А - точка приложения силы
зависит от выбора центра О (или начала, или полюса). Точка А - точка приложения силы 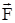 . Модуль вектора момента силы относительно полюса О можно определить произведением модуля силы на плечо. Плечо (L) - длина перпендикуляра, опущенного из точки О на линию действия силы.
. Модуль вектора момента силы относительно полюса О можно определить произведением модуля силы на плечо. Плечо (L) - длина перпендикуляра, опущенного из точки О на линию действия силы.
 Действительно,
Действительно, 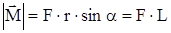 , (7)
, (7)
где 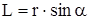 - плечо силы F. Момент силы
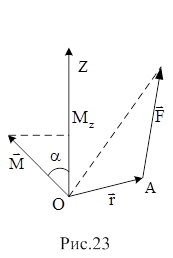
- плечо силы F. Момент силы 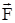 относительно некоторой оси (Z) - это проекция на ось вектора
относительно некоторой оси (Z) - это проекция на ось вектора 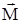 , взятого относительно какой - либо точки О на оси (рис.23).
, взятого относительно какой - либо точки О на оси (рис.23).
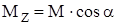 . (8)
. (8)
Следует отметить, что момент силы относительно оси не зависит от выбора точки О, лишь бы она находилась на этой оси. Момент силы относительно оси - величина алгебраическая, причем его знак зависит как от выбора положительного направления Z, так и от направления вращения соответствующего момента силы.
Для вращательного движения существенное значение имеет распределение массы по объему твердого тела, и инертные свойства твердого тела при вращательном движении определяются моментом инерции.
Момент инерции твердого тела относительно оси равен сумме произведений элементарных масс тела на квадраты их расстояний до оси вращения, т.е.
 . (9)
. (9)
Вычисление момента инерции тела производится по формуле:
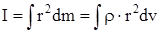 , (10)
, (10)
где dm и dv - элементарные массы и объем, находящиеся на расстоянии r от
оси вращения,
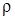 - плотность тела в данной точке.
- плотность тела в данной точке.
Но во многих случаях определение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси равен моменту инерции Ic относительно оси, параллельно данной и проходящей через центр масс (С) тела, плюс произведение массы (m) тела на квадрат расстояния (d) между осями:
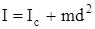 . (11)
. (11)
В случае вращения твердого тела вокруг неподвижной оси уравнение динамики вращательного движения имеет вид (при условии, что момент инерции Iz=const)
 , (12)
, (12)
т.е. произведение момента инерции (Iz) твердого тела относительно неподвижной оси вращения на угловое ускорение (e) равно моменту внешних сил относительно этой же оси.
Угловое ускорение равно:
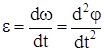 . (13)
. (13)
Рассмотрим один важный случай движения твердого тела вокруг закрепленной оси, когда момент внешних сил обусловлен действием силы тяжести.
Физическим маятником называется твердое тело, которое совершает колебание около неподвижной точки (т.О, рис.24), не совпадающей с центром масс маятника (т.С). Положение тела в каждый момент времени можно характеризовать углом отклонения j из положения равновесия.
Момент (М) силы тяжести относительно оси вращения, проходящей через точку О, равен
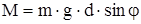 , (14)
, (14)
где d - расстояние от оси вращения до центра масс.
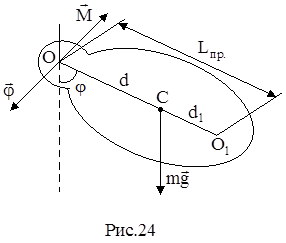 Вектор
Вектор 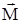 проходит через т.О и направлен перпендикулярно плоскости чертежа от нас (согласно правилу правого винта).
проходит через т.О и направлен перпендикулярно плоскости чертежа от нас (согласно правилу правого винта).
Вектор угла поворота j твердого тела имеет направление, противоположное направлению вектора 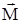 (рис.24). Поэтому уравнение динамики вращательного движения (12) с учетом (13) в данном случае имеет вид:
(рис.24). Поэтому уравнение динамики вращательного движения (12) с учетом (13) в данном случае имеет вид:
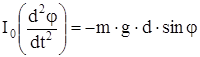 , (15)
, (15)
где I0 - момент инерции твердого тела относительно оси вращения, проходящей через точку О.
Учитывая, что  и при малых углах отклонения
и при малых углах отклонения 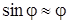 , уравнение вращательного движения маятника (15) принимает вид:
, уравнение вращательного движения маятника (15) принимает вид:
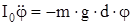 или
или 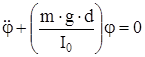 . (16)
. (16)
Выражение (16) является дифференциальным уравнением гармонического колебания маятника, круговая частота которого равна:
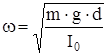 . (17)
. (17)
Учитывая, что период* гармонических колебаний связан с круговой частотой соотношением
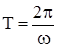 ,
,
получим выражение для периода малых колебаний физического маятника
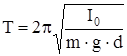 . (18)
. (18)
Частным случаем физического маятника является математический маятник - это небольшое тело, подвешенное на невесомой, нерастяжимой и столь длинной нити, что размерами тела можно пренебречь по сравнению с длиной нити (масса маятника практически сосредоточена в одной точке).
Применяя уравнение моментов (12) (уравнение динамики вращательного движения) к задаче о движении математического маятника и осуществив преобразования, как и в случае физического маятника, получим формулу периода колебаний математического маятника
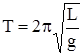 , (19)
, (19)
где L - длина нити.
Из сравнения формул (18) и (19) следует, что физический маятник колеблется так же, как математический маятник с длиной нити
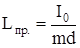 , (20)
, (20)
которая называется приведенной длиной физического маятника.
Отложим от точки подвеса О (рис.24) вдоль прямой ОС отрезок ОО1, длина которого равна приведенной длине физического маятника Lпр. Точка О1 называется центром качаний данного физического маятника.
Центр качаний можно определить как материальную точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.
Приведенная длина Lпр всегда больше d, т.е. центр качаний всегда лежит ниже центра масс C (рис.24). Действительно, по теореме Штейнера момент инерции относительно оси маятника равен
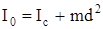 ,
,
где Ic - момент инерции маятника относительно параллельной оси, проходящей через центр масс С.
Подставив последнее выражение в (20), получим:
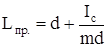 . (21)
. (21)
Следует отметить, что точка подвеса и центр качаний находятся по разные стороны от центра масс и расположены асимметрично относительно него.* Точка подвеса и центр качаний являются обратимыми (взаимными, сопряженными) точками физического маятника. Если перенести точку подвеса физического маятника в центр качаний, то прежняя точка подвеса окажется новым центром качаний. Это положение, называемое также теоремой Штейнера, доказывается следующим образом:
Пусть d1=CO1 (рис.24) и маятник подвешен за точку О1. При этом (по аналогии с(21))приведенная длина маятника становится равной
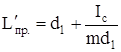 ,
,
где 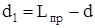 или с учетом (21)
или с учетом (21) 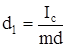 .
.
Отсюда следует, что  и
и 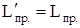 .
.
Итак, приведенная длина, следовательно, и период колебаний физического маятника остались без изменения. На этом свойстве основано устройство оборотного маятника, применяемого для определения ускорения силы тяжести.
Если использовать соотношение (18) для определения ускорения свободного падения 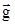 , то с высокой точностью можно измерить только период колебаний Т маятника, а величины I0 и d, входящие в формулу (18), достаточно точно измерить не удается. Преимуществом метода оборотного маятника для определения ускорения свободного падения является то, что величины момента инерции I0 и расстояния d между точкой подвеса и центром масс можно исключить при экспериментальном определении величины g. Формула (18) с учетом (20) и (21) принимает вид:
, то с высокой точностью можно измерить только период колебаний Т маятника, а величины I0 и d, входящие в формулу (18), достаточно точно измерить не удается. Преимуществом метода оборотного маятника для определения ускорения свободного падения является то, что величины момента инерции I0 и расстояния d между точкой подвеса и центром масс можно исключить при экспериментальном определении величины g. Формула (18) с учетом (20) и (21) принимает вид:
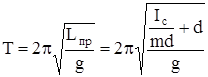 . (22)
. (22)
Как указывалось выше, при расстояниях d и d1 периоды колебаний маятника должны быть равными, т.е.
T(d) = T(d1).