Физические свойства жидкостей и газов.

Понятие плотности сплошной среды. Объемные свойства жидкостей и газов. Вязкость жидкостей и газов. Явления на границах жидкостей с газами и твердыми телами. Испарение и кипение жидкостей.

Согласно гипотезе сплошности масса среды распределена в объеме непрерывно и в общем неравномерно. Основной динамической характеристикой среды является плотность распределения массы по объему или просто плотность среды, которая в произвольной точке A определяется соотношением

, (1.1)

Где 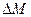- масса, заключенная в малом объеме 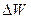, включающем точку A - предел берется при стягивании объема 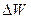к этой точке.

Размерность плотности

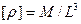
Где М - размерность массы; L - размерность длины.

Единицами измерения плотности являются в системе СИ и 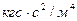в технической системе.

Наряду с плотностью в рассмотрение вводится понятие удельного объема 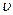, который представляет собой объем, содержащий единицу массы:

. (1.2)

Плотность среды может изменяться от точки к точке и в данной точке со временем, т. е. 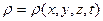. Однако эта функциональная связь не является непосредственной, так как плотность жидкостей и газов определяется фактически значениями термодинамических параметров состояния ( 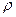и ), которые при движении среды зависят от координат 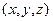и времени .

Связь между плотностью, температурой и давлением устанавливается уравнением состояния, которое для реальных жидкостей выводится в кинетической теории. Из-за сложности общего уравнения состояния и трудности определения, входящих в него констант для качественного анализа свойств этих сред пользуются приближенными теоретическими или эмпирическими уравнениями. Широкое применение получило, например, уравнение Ван-дер-Ваальса

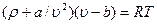, (1.3)

где a, b и R - константы для данной среды.

Это уравнение, выведенное в кинетической теории газов, является приближенным, но качественно верно отражает полученные опытным путем закономерности.

На рис. 1.1 изображены изотермы Ван-дер-Ваальса, выражающие зависимости удельного объема от давления при различных постоянных температурах. Жидкому состоянию соответствует участок , а газообразному ‑ участок . Как показывают кривые и , с увеличением давления объем жидкостей и газов уменьшается. Разные наклон и кривизна этих участков свидетельствуют о разной степени сжимаемости рассматриваемых сред.

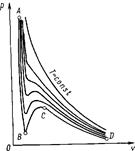
Рис. 1.1 ‑ Изотермы Ван-дер-Ваaльса

Количественно сжимаемость оценивают изотермическим коэф-фициентом сжимаемости

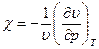. (1.4)

Для жидкостей производная 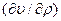мало отличается от нуля [обычно 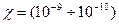1/Па], что свидетельствует об их малой сжимаемости. Для всех жидкостей χ уменьшается с возрастанием давления и увеличивается с повышением температуры.

Из уравнения Ван-дер-Ваальса можно получить выражение для коэффициента сжимаемости, но из-за приближенности этого уравнения практическое применение получили выражения χ найденные опытным путем.

Соотношение (1.4) можно представить в другом виде, заменив 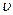на и обозначив 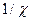через S:

(1.5)

Величина 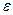называется модулем упругости жидкости. Для воды при нормальных условиях 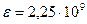Па. В форме (1.5) уравнение сжимаемости выражает закон Гука для жидкостей.

Для совершенных газов соотношение между 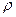и 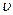приближенно описывается уравнением Клайперона

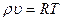, (1.6)

откуда, учитывая, что T = const, получаем

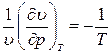
Следовательно, изотермический коэффициент сжимаемости газов определяется формулой

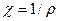, (1.7)

при этом изотермический модуль упругости газов

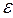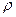= . (1.8)

Формулы (1.7) и (1.8) свидетельствуют о высокой сжимаемости газов.

Объем жидкостей и газов изменяется при изменении не только давления, но и температуры. Как правило, жидкости и газы расширяются с повышением температуры, а плотность их при этом уменьшается. Исключение составляет вода, плотность которой возрастает при повышении температуры от 0 до 4 и достигает максимума при 4 . Такая аномалия объясняется особенностями молекулярного строения воды.

Количественно изменение объема при изменении температуры и постоянном давлении оценивается коэффициентом теплового объемного расширения

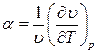(1.9)

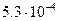У жидкостей этот коэффициент зависит от температуры и давления, возрастая с повышением первой и уменьшаясь с увеличением второго. При нормальных условиях для этилового спирта равно , для глицерина , для ртути 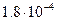, для воды 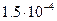1/К.

Для газов из уравнения (1.6) при 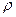= const получаем

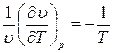
т. е.

.

Исходя из общего уравнения состояния 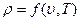, можно показать, что между коэффициентами сжимаемости и объемного теплового расширения существует связь вида

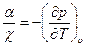
где производная 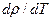вычисляется при постоянном объеме.

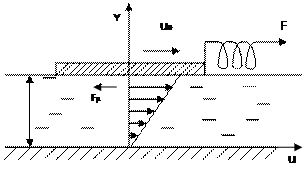
Как уже известно, молекулярные движения в жидкостях и газах обусловливают сопротивление этих сред сдвигающим усилиям. Наличие силы сопротивления при сдвиге можно обнаружить из опыта (рис. 1.2). На неподвижной нижней пластинке находится слой жидкости толщиной 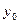, на свободной поверхноти ‑ легкая пластинка площадью S. Если к пластинке приложить силу F, она начнет перемещаться. После некоторого «разгонного» интервала времени установится равномерное движение пластинки с некоторой скоростью 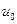. Это означает, что за время разгона возникает приложенная к пластинке сила 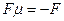. Она может быть только силой сопротивления жидкости.

Рис. 1.2. Схема для определения силы вязкости

Механизм возникновения силы сопротивления можно представить следующим образом. Слой жидкости, прилегающей к пластинке, прилипает к ней и движется вместе с пластинкой со скоростью 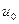. Вследствие молекулярных связей этот слой увлекает за собой следующий и т. д. Поскольку нижний слой примыкает к неподвижной пластинке, его скорость равна нулю. Таким образом, в жидкости возникает слоистое движение с некоторым распределением скоростей по высоте .

В рассматриваемом случае распределение скоростей линейное. Вследствие действия межмолекулярных связей между движущимися слоями жидкости возникает сила 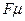вязкости или внутреннего трения. Для рассматриваемого движения с линейным распределением скоростей по толщине слоя

.

Но в более общем случае при произвольном профиле скорости современная запись закона внутреннего (вязкого) трения Ньютона имеет вид

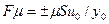(1.10)

где 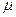‑ динамический коэффициент вязкости; S ‑ площадь соприкосновения слоев; 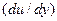‑ градиент скорости, являющийся показателем интенсивности ее изменения по нормали к ее направлению; знак «+» или «‑» выбирают в зависимости от знака градиента скорости и направления силы .

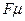Вязкое или касательное напряжение

. (1.11)

Как указано выше, газы также обладают вязкостью, но механизм межмолекулярного взаимодействия, проявляющегося в этом свойстве, в них иной, нежели в жидкостях. Исходя из представлений о молекулярной структуре жидкостей, можно предположить, что в этих средах при повышении температуры возрастает кинетическая энергия колебательных движений молекул, учащаются их «перескоки», в результате чего облегчается относительный сдвиг слоев. Макроскопически это обнаруживается в уменьшении вязкости.

В газах вязкость обусловлена хаотическим движением молекул, благодаря которому происходит обмен количеством движения. При относительном сдвиге слоев газа этот обмен создает тенденцию к выравниванию скоростей, т. е. препятствует сдвигу и порождает силу внутреннего трения (вязкости). Для совершенного газа напряжение 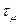можно определить, применив теорему импульсов к массе молекул, пересекающих единичную площадку на поверхности раздела сдвигаемых слоев. В результате получается формула, имеющая такую же структуру, как и формула (1.11). Следовательно, последняя справедлива как для жидкостей, так и для газов, и различие этих сред проявляется только в закономерностях изменения коэффициента вязкости.

Динамический коэффициент вязкости 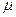, являющийся основной количественной характеристикой вязкости жидкостей и газов, имеет размерность

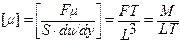
где F ‑ размерность силы; Т ‑ размерность времени.

Единицами измерения для 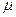являются 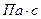в системе СИ; 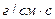(пуаз) в системе СГС и 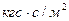в технической системе.

Наряду с динамическим коэффициентом вязкости в механике жидкости и газа широко используют кинематический коэффициент вязкости v.

Легко убедиться, что

.

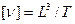Единицами измерения кинематического коэффициента вязкости являются 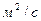и (стокс).

В соответствии с качественно описанным выше механизмом возникновения вязкости в жидкостях и газах динамическая вязкость сильно зависит от температуры, причем для жидкостей при повышении температуры она уменьшается, а для газов - возрастает. Давление мало влияет на значения .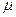

Для воды Пуазейлем получена формула

,

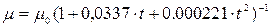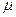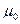где и — динамический коэффициент вязкости при температурах t и .

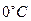Для газов можно воспользоваться формулой Сатерленда

,

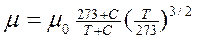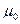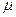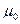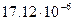
где C ‑ постоянная, зависящая от рода газа; Т ‑ термодинамическая температура; - значение при ; для воздуха = 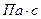; С = 111.

На рис. 1.3 приведены зависимости кинематического коэффициента вязкости воды, машинного масла и воздуха от температуры.

Условия, в которых находятся молекулы покоящейся жидкости на границах с газами, другими жидкостями или твердыми телами, отличаются от условий, в которых находятся молекулы внутри жидкого объема. Во втором случае частицы со всех сторон подвержены воздействию соседних частиц с теми же свойствами, поэтому все силы, действующие на рассматриваемую частицу, уравновешиваются. Если же молекулы расположены на границе, то силы, действующие со стороны граничного тела, могут отличаться от сил, действующих внутри объема жидкости.

Система сил оказывается неуравновешенной, и появляется равнодействующая, направленная внутрь или наружу объема жидкости. Чтобы жидкость находилась в покое, эта равнодействующая должна уравновешиваться некоторой иной силой.

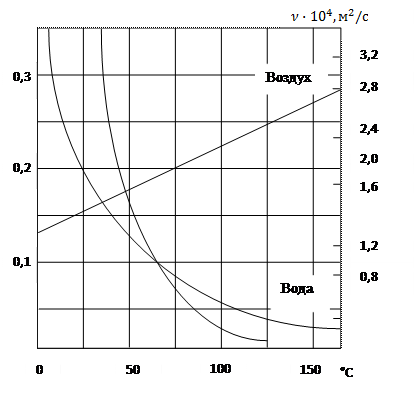
Рис. 1.3. Зависимость кинематического коэффициента вязкости воды машинного масла и воздуха от температуры

Если указанная сила, испытываемая молекулами поверхностного слоя, направлена внутрь жидкости, то для перемещения частицы изнутри объема на поверхность необходимо затратить некоторую энергию, т. е. выполнить работу. Это значит, что молекулы поверхностного слоя имеют избыточную по сравнению с внутренними молекулами потенциальную энергию. Энергия 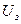молекул пропорциональна площади поверхности S, занимаемой этими молекулами:

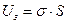. (1.13)

Величина 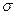называется коэффициентом поверхностного натяжения.

Система, находящаяся в равновесии, занимает то из возможных для нее положений, которое соответствует минимуму энергии. Следовательно, жидкость в равновесии имеет минимальную поверхность, т. е. существуют силы, стремящиеся уменьшить последнюю. Они направлены по касательной к этой поверхности. Эти силы обнаруживаются простыми опытами и называются силами поверхностного натяжения.

Если выбрать на свободной поверхности жидкости некоторую линию длиной 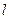и приложить к поверхности распределенную по этой линии и нормальную к ней, но касательную к поверхности внешнюю силу 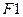то сила поверхностного натяжения 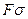будет препятствовать разрыву (разделу) поверхности вдоль этой линии. Пусть в результате действия такой внешней силы поверхность по нормали к линии длиной 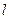растянулась на величину 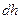. Тогда изменение поверхностной энергии 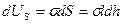должно равняться работе приложенной силы 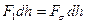, т. е.

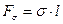. (1.14)

Следовательно, коэффициент поверхностного натяжения, а есть сила, действующая по касательной к поверхности жидкости и приходящаяся на единицу длины 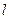линии раздела.

Единицами измерения, а являются Н/м в системе СИ, и дин/см в системе СГС.

Благодаря действию сил поверхностного натяжения объем жидкости, на который не действуют никакие другие силы, принимает сферическую форму. Это было подтверждено во время космических полетов и в земных условиях.

Со свойством поверхностного натяжения связана способность жидкостей образовывать капли, из-за которой обычные жидкости иногда называют капельными.

На границе между жидкостью и твердым телом возникают силы взаимодействия между молекулами этих двух сред. Соотношение между этими силами и силами взаимодействия между молекулами самой жидкости определяет характер граничных явлений. Если на твердую горизонтальную плоскость поместить каплю жидкости, то возможны случаи:

а) полного растекания жидкости по твердой поверхности тонким слоем (полное смачивание), когда краевой угол 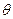= 0 (рис. 1.4, а);

б) частичного смачивания, когда краевой угол 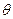< 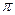/2 (рис. 1.4, б);

в) частичного несмачивания, когда 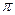/2 < 0 < 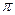(рис. 1.4, а);

г) полного несмачивания, когда 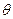= 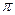(рис. 1.4, г).

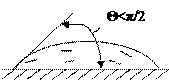
а) б) в) г)

Рис. 1.4. Возможные случаи смачивания твердой поверхности вязкой жидкостью.

Хотя существует несмачивание, но при движении жидкости скорости частиц, соприкасающихся с твердой поверхностью, в большинстве случаев равны скорости последней. Этот факт для гидродинамики весьма важен, так как на нем основана формулировка граничных условий при математической постановке гидродинамических задач.

Силы молекулярного взаимодействия между жидкостью и твердыми стенками создают искривление свободной поверхности вблизи этих стенок. В трубке малого диаметра (капилляре) поверхность может быть или вогнутой (смачивание) или выпуклой (несмачивание). Искривление свободной поверхности сопровождается появлением дополнительного давления, в результате чего уровень в таких трубках поднимается или понижается. Высота капиллярного подъема жидкости

,

где g ‑ ускорение свободного падения; r ‑ радиус трубки.

Из формулы следует, что при малых r подъем может быть значительным.

Переход жидкости в пар называется испарением, а обратный переход ‑ конденсацией. Жидкость может находиться в равновесии со своим паром. Это равновесие наступает само собой, если жидкость длительное время заключена в закрытом сосуде. Тогда с течением времени достигается такое состояние, при котором число молекул, переходящих из жидкости в пар, равно числу молекул, совершающих обратный переход. В этом случае пар называют, насыщенным и в нем устанавливается вполне определенное при данной температуре давление, называемое упругостью насыщенного пара. Эта величина возрастает с увеличением температуры.

Образование насыщенных паров приводит к тому, что на свободной поверхности жидкости не может быть достигнуто давление ниже упругости насыщенного пара, соответствующей данной температуре.

Жидкость может испаряться не только со свободной поверхности, но и внутрь пузырей, образующихся в ней при определенных температуре и давлении. Такой фазовый переход называется кипением. Оно может наступить в покоящейся или движущейся жидкости при температуре, равной температуре кипения при данном давлении, или при давлении, равном упругости насыщенного пара при данной температуре.

Как показывают физические исследования, кипение возникает лишь в том случае, если в жидкости имеются пузырьки защемленного у стенок газа или если такие пузырьки образуются вследствие выделения газа, растворенного в жидкости. Тогда при повышении температуры или понижении давления жидкость испаряется внутрь пузырьков, они растут в объеме и прорываются наружу через свободную поверхность. Возникает процесс кипения.

Если жидкость освобождена от растворенного и защемленного газа, то процесс кипения не возникает даже при температуре, значительно превосходящей температуру кипения. Жидкости в таком состоянии называют перегретыми. Дегазированные жидкости не кипят и при понижении давления ниже упругости насыщенных паров. Доказано, что такие жидкости могут выдерживать значительные растягивающие напряжения.

Однако в технике приходится, как правило, иметь дело с жидкостями, в которых есть растворенный или защемленный в виде пузырьков газ. Технические жидкости не только не выдерживают растягивающих усилий, но и вскипают при давлениях, равных упругости насыщенных паров.

Кипение жидкостей приводит к нарушению сплошности среды, поэтому значения параметров, при которых оно наступает, определяют границу применимости всех выводов, основанных на гипотезе сплошности.

Для механики жидкости и газа (далее МЖиГ) особый интерес представляет частный случай кипения, которое возникает в движущейся жидкости вследствие местных понижений давления до давления насыщенного пара. Такой вид кипения называют кавитацией. Последняя играет особую и главным образом отрицательную роль в гидродинамике машин и аппаратов и других технических приложениях. Кавитация может проявляться как в виде отдельных пузырьков, возникающих в местах пониженного давления и уносимых потоком (пузырьковая перемещающаяся кавитация), так и в виде сплошных, заполненных парами жидкости, полостей, присоединенных к поверхности обтекаемых тел (суперкавитация). Могут существовать и другие внешние проявления кавитации.

Кавитация, как правило, сопровождается изменением закономерностей течения в связи с нарушением сплошности, а также разрушением материала твердых стенок при схлопывании пузырьков вблизи границ течения. Некоторые гидродинамические устройства (например, измерители расхода жидкости) при появлении кавитации становятся неработоспособными. Исследование причин и механизма кавитационных разрушений лопастей гидравлических турбин, насосов, гребных винтов представляет собой одну из важных технических проблем.

Поведение жидкости при понижении давления существенно зависит от наличия в ней растворенного газа. Закономерность растворения газов в жидкостях в первом приближении устанавливается законом Генри, согласно которому концентрация газа, растворенного в жидкости, пропорциональна его давлению над раствором.