Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Плоскость в пространстве.
|
|
Общим уравнением плоскости в пространстве называется уравнение
 .
.
Вектор  называется нормальным вектором плоскости. Если даны две плоскости с нормальными векторами
называется нормальным вектором плоскости. Если даны две плоскости с нормальными векторами 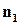 и
и 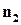 , то косинус угла между этими плоскостями определяется по формуле (этот угол всегда острый или прямой)
, то косинус угла между этими плоскостями определяется по формуле (этот угол всегда острый или прямой)
 .
.
Если даны три точки  ,
, 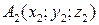 и
и  , то уравнение плоскости, проходящей через три точки находится по формуле:
, то уравнение плоскости, проходящей через три точки находится по формуле:
 .
.
Задание 1. По координатам вершины пирамиды  найти:
найти:
1. длину ребер 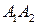 и
и 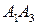 ;
;
2. угол между ребрами  и
и 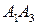 ;
;
3. площадь грани 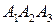 ;
;
4. объем пирамиды 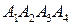 ;
;
5. уравнение прямых  ;
; 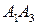 ;
;
6. уравнения плоскостей 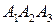 и
и 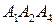 ;
;
7. угол между плоскостями 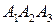 и
и 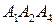 .
.
Пример. Выполнить задание 1, если  ,
,  ,
,  ,
,  .
.
1) Если заданы точки  ,
,  , и
, и  то координаты векторов
то координаты векторов  ,
, 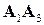 и их длины
и их длины  ,
, 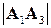 равны:
равны:
а) 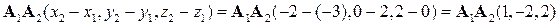 ,
,
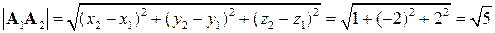 .
.
б) 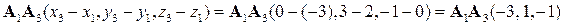 ,
,
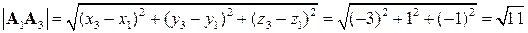 .
.
2) Угол между ребрами  и
и 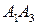 находим как угол между векторами
находим как угол между векторами 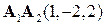 и
и  . Из определения скалярного произведения следует, что этот угол вычисляется по формуле:
. Из определения скалярного произведения следует, что этот угол вычисляется по формуле:
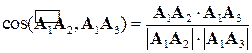 .
.
Скалярное произведение 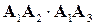 находим через декартовы координаты:
находим через декартовы координаты:
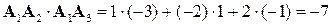 .
.
Тогда
 .
.
Откуда (вычисления проводим на инженерном калькуляторе)
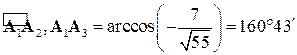
3)  ‑ площадь треугольника, построенного на векторах
‑ площадь треугольника, построенного на векторах  и
и 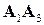 . Зная их декартовы координаты, находим векторное произведение
. Зная их декартовы координаты, находим векторное произведение
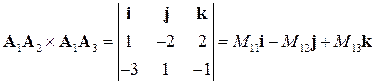 ,
,
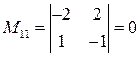 ,
, 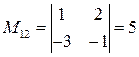 ,
, 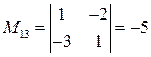 .
.
Тогда
 .
.
4) Учитывая геометрический смысл смешанного произведения векторов, получим формулу для вычисления объема пирамиды:
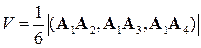 .
.
Найдем координаты вектора 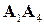 :
:

Смешанное произведение этих векторов найдем через их декартовы координаты
 .
.
Отсюда
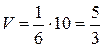 .
.
5) Найдем канонические уравнение прямых  и
и 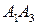 . За направляющие вектора примем вектора
. За направляющие вектора примем вектора 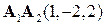 и
и 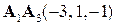 . За точку лежащую на этих векторах примем точку
. За точку лежащую на этих векторах примем точку 
прямая  :
:  ;
;
прямая 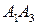 :
: 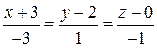 .
.
6) Уравнение плоскости, проходящей через три точки 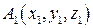 ,
, 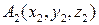 и
и 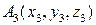 находится по формуле:
находится по формуле:
 .
.
Составимуравнение плоскости, проходящей через три точки  ,
,  ,
,  .
.
 или
или 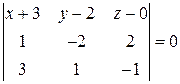 .
.
Разложив определить по первой строке, получим
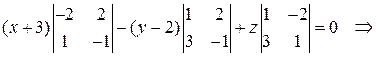
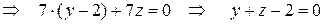 .
.
Итак, уравнение плоскости 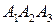 найдено
найдено  . Коэффициенты уравнения образуют нормальный вектор
. Коэффициенты уравнения образуют нормальный вектор 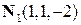 .
.
Аналогично составимуравнение плоскости, проходящей через три точки  ,
,  ,
,  .
.
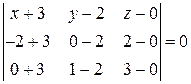 или
или 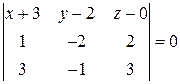 .
.
Разложив определить по первой строке, получим
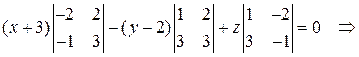
 .
.
Итак, уравнение плоскости 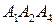 имеет вид
имеет вид 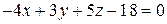 . Коэффициенты уравнения образуют нормальный вектор
. Коэффициенты уравнения образуют нормальный вектор 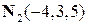 .
.
7) Угол 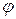 , образованный двумя плоскостями
, образованный двумя плоскостями 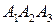 и
и 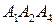 находится по формуле
находится по формуле
 , где
, где 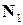 и
и  ‑ нормали плоскостей
‑ нормали плоскостей 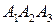 и
и 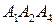 .
. 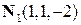
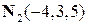
Подставляя их значения из пункта 6) находим величину угла 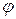 (расчеты выполняем на инженерном калькуляторе)
(расчеты выполняем на инженерном калькуляторе)