
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример.
|
|
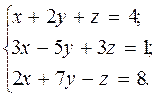
а) Составим и вычислим главный и вспомогательные определители системы:
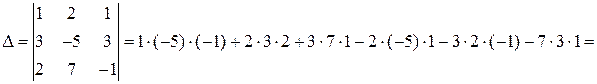
 ,
,
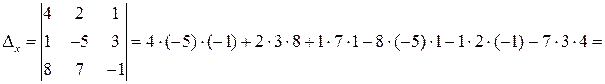
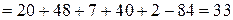 ,
,

 ,
,

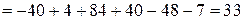 .
.
Находим по правилу Крамера решение системы
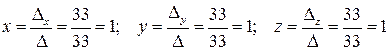 .
.
б) Составим матрицу коэффициентов системы и столбец правых частей
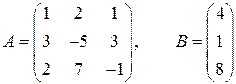 ,
,
и найдем обратную матрицу по формуле:
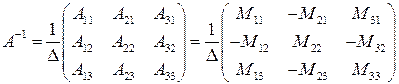 ,
,
где 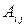 и
и 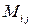 ‑ соответственно алгебраические дополнения и миноры, связанные между собой соотношением
‑ соответственно алгебраические дополнения и миноры, связанные между собой соотношением 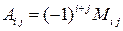 , а
, а 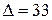 - определитель матрицы
- определитель матрицы  , вычисленный в пункте а). Найдем миноры:
, вычисленный в пункте а). Найдем миноры:
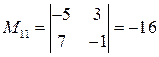 ;
; 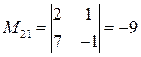 ;
; 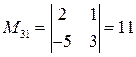 ;
;
 ;
; 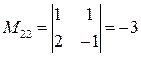 ;
; 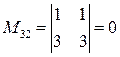 ;
;
 ;
;  ;
; 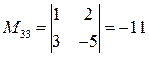 .
.
Составим теперь обратную матрицу

и найдем столбец неизвестных по формуле 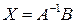 :
:
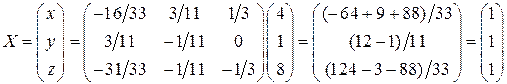 .
.
Отсюда 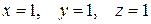 .
.
Задание №3. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления
При вычислении предела дробно-рациональной функции при 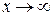 числитель и знаменатель дроби — величины бесконечно большие, т.е. получаем выражение
числитель и знаменатель дроби — величины бесконечно большие, т.е. получаем выражение 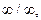 которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень
которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень 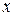 .
.
Пример 1.  .
.
Для вычисления предела этой функции нужно числитель и знаменатель разделить на 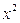 :
:
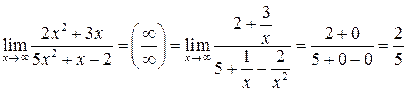 .
.
(при 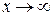 слагаемые
слагаемые 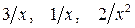 — величины бесконечно малые и, следовательно, их пределы равны нулю).
— величины бесконечно малые и, следовательно, их пределы равны нулю).
В том случае, когда при вычислении предела дробно-рациональной функции при  числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность
числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность  , надо разделить их на
, надо разделить их на  и перейти к пределу. Если после деления окажется, что при
и перейти к пределу. Если после деления окажется, что при  числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на
числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на  .
.
Пример 2.  .
.
Данный предел имеет неопределенность вида  , так как числитель и знаменатель при
, так как числитель и знаменатель при 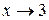 стремятся к 0. Разложим квадратные трёхчлены в числителе и знаменателе рациональной дроби на линейные множители по формуле
стремятся к 0. Разложим квадратные трёхчлены в числителе и знаменателе рациональной дроби на линейные множители по формуле  , где
, где 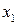 и
и  — корни квадратного трёхчлена
— корни квадратного трёхчлена
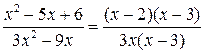 .
.
Сократив рациональную дробь на  , получим:
, получим:
 .
.
При вычислении пределов тригонометрических функций часто используется первый замечательный предел
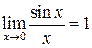
и его следствия:
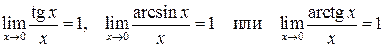 .
.
Пример 3.  .
.
Преобразовав разность косинусов в произведение, получим
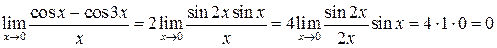 .
.
Если в пределе встречается неопределенность 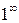 , то используется второй замечательный предел
, то используется второй замечательный предел 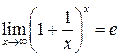 или
или 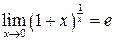 .
.
Пример 4.  .
.
Выполнив преобразования и применив второй замечательный предел, найдём
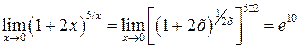 .
.
Пример 5. 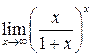 .
.
Выполнив преобразования и применив формулу 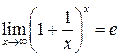 , найдём
, найдём
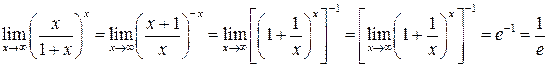 .
.
Задание №4. Исследовать функцию на непрерывность. Найти точки разрыва функции и определить их тип.
Функция  называется непрерывной в точке
называется непрерывной в точке 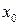 , если предел функции в этой точке равен значению функции в этой точке, т.е.
, если предел функции в этой точке равен значению функции в этой точке, т.е.
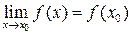 .
.
Это равенство означает выполнение трех условий:
1) функция 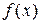 определена в точке х0 и ее окрестности;
определена в точке х0 и ее окрестности;
2) функция 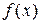 имеет предел при
имеет предел при 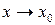 ;
;
3) предел функции в точке 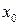 равен значению функции в этой точке
равен значению функции в этой точке
Если в точке 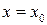 не выполняется по крайней мере одно из условий определения непрерывности функции, то такая точка называется точкой разрыва. Все точки разрыва разделяются на точки разрыва первого и второго рода.
не выполняется по крайней мере одно из условий определения непрерывности функции, то такая точка называется точкой разрыва. Все точки разрыва разделяются на точки разрыва первого и второго рода.
Точка разрыва х0 называется точкой разрыва первого рода функции  , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. 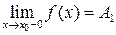 и
и 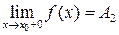 .
.
При этом:
1) если 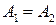 , то точка х0 называется точкой устранимого разрыва;
, то точка х0 называется точкой устранимого разрыва;
2) если 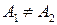 , то х0 называется точкой конечного разрыва, а величину
, то х0 называется точкой конечного разрыва, а величину  называют скачком функции.
называют скачком функции.
Точка разрыва х0 называется точкой разрыва второго рода функции  , если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.
, если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.