
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. Производная функции, заданной параметрически, вычисляется по формуле:
|
|
1) 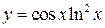 .
.

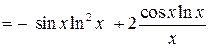 .
.
2)  .
.
 .
.
3)  Найти
Найти  .
.
Производная функции, заданной параметрически, вычисляется по формуле:  .
.
 ;
;  .
.
Тогда  .
.
Задание №6. Составить уравнения касательной и нормали к графику функции  , проведенных в данной точке
, проведенных в данной точке  .
.
Приведем уравнение касательной, проведенной к графику функции  в точке
в точке 
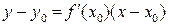 ,
,
и уравнение нормали к этой касательной
 .
.
Пример.
Для функции 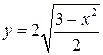 в точке с абсциссой
в точке с абсциссой 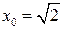 составить уравнение касательной и уравнение нормали.
составить уравнение касательной и уравнение нормали.
1) Найдем значение функции  .
.
2) Найдем значение 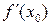 :
:
 ,
,  .
.
3) Составим уравнения касательной и нормали:
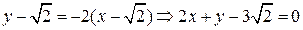 – искомое уравнение касательной;
– искомое уравнение касательной;
 – искомое уравнение нормали.
– искомое уравнение нормали.
Задание №7. Найти предел функции с помощью правила Лопиталя.
Напомним правило Лопиталя для раскрытия неопределенностей вида  и
и  :
:
Пусть 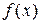 и
и 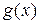 – функции, имеющие производные в некоторой окрестности точки
– функции, имеющие производные в некоторой окрестности точки  , за исключением, быть может, самой
, за исключением, быть может, самой  точки
точки  . Пусть при стремлении
. Пусть при стремлении  обе эти функции стремятся одновременно к нулю или к бесконечности. Тогда, если существует предел отношения их производных
обе эти функции стремятся одновременно к нулю или к бесконечности. Тогда, если существует предел отношения их производных 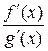 при
при  , то существует и предел отношения самих функций
, то существует и предел отношения самих функций  при
при  , причем оба эти пределы равны:
, причем оба эти пределы равны:
 .
.
Замечания:
1) Правило Лопиталя остается справедливым и в том случае, если 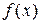 и
и 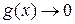

 или
или  при
при  или при
или при  .
.
2) Если  опять дает неопределенность вида
опять дает неопределенность вида  или
или  , то правило Лопиталя следует применить еще раз.
, то правило Лопиталя следует применить еще раз.
Примеры:
1)  .
.
2)  .
.
3)  .
.
Задание №8. Построить график функции  , используя общую схему исследования функций.
, используя общую схему исследования функций.
Общая схема исследования функции и построения графика.
1. Найти область определения функции.
2. Определить тип функции (четность, нечетность).
3. Найти точки пересечения с осями координат и интервалы знакопостоянства функции.
4. Найти асимптоты графика функции:
а) вертикальные; б) невертикальные (наклонные).
5. Найти точки возможного экстремума и интервалы возрастания и убывания функции.
6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.
7. Построить график функции, учитывая проведенные исследования.
Пример. Построить график функции  .
.
1. Областью определения функции является множество всех действительных чисел, кроме 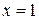 (в этом случае знаменатель равен нулю).
(в этом случае знаменатель равен нулю).
2. Для определения типа функции найдем значение
 .
.
Следовательно, функция  не является ни четной ни нечетной.
не является ни четной ни нечетной.
3. Так как уравнение  не имеет действительных корней, то график функции не имеет точек пересечения с осью ОХ, но пересекает ось ОУ в точке
не имеет действительных корней, то график функции не имеет точек пересечения с осью ОХ, но пересекает ось ОУ в точке 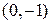 .
.
Определим интервалы знакопостоянства функции:
 .
.
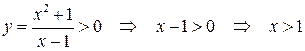 .
.
 4. Найдем асимптоты графика функции.
4. Найдем асимптоты графика функции.
а) Исследуем поведение функции вблизи точки разрыва 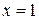 :
:
 ,
,  .
.
Следовательно прямая 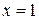 является вертикальной асимптотой.
является вертикальной асимптотой.
б). Определим существование наклонной асимптоты:
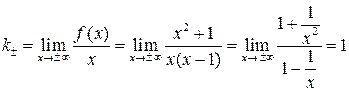 ,
,
 .
.
Следовательно, график функции имеет наклонную асимптоту  при
при  .
.
5. Для нахождения точек возможного экстремума найдем производную функции:
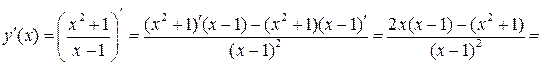
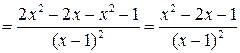 .
.
Приравняем  . Решая уравнение
. Решая уравнение  , находим корни производной
, находим корни производной  и
и 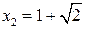 .
.
Исследуем знак производной. Для чего решим неравенство 
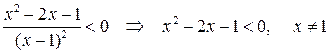
Находим знаки  на промежутках, учитывая корни
на промежутках, учитывая корни  и
и 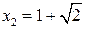 квадратного трехчлена
квадратного трехчлена 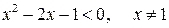 :
:
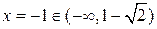 ,
,  ;
;  ,
, 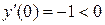 ;
;
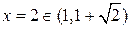 ,
, 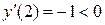 ;
;  ;
;  .
.
Следовательно, функция возрастает на промежутках
 и
и 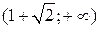 ,
,
и убывает на промежутках
 и
и 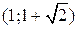 .
.
По изменению знака  получаем точки локальных экстремумов:
получаем точки локальных экстремумов:
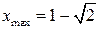 ,
,  ,
,
 ,
, 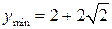 .
.
6. Для нахождения точек перегиба и интервалов выпуклости, вогнутости найдем вторую производную функции:

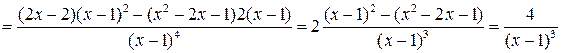 .
.
Так как  в нуль не обращается, то точек перегиба у функции нет.
в нуль не обращается, то точек перегиба у функции нет.
Исследуем знак второй производной, решая неравенство  :
:
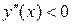 при
при  и
и  при
при 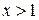 .
.
 Следовательно, на интервале
Следовательно, на интервале 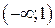 график направлен выпуклостью вверх (выпуклый), а на интервале
график направлен выпуклостью вверх (выпуклый), а на интервале  – выпуклостью вниз (вогнутый).
– выпуклостью вниз (вогнутый).
По результатам исследования строим график функции  .
.
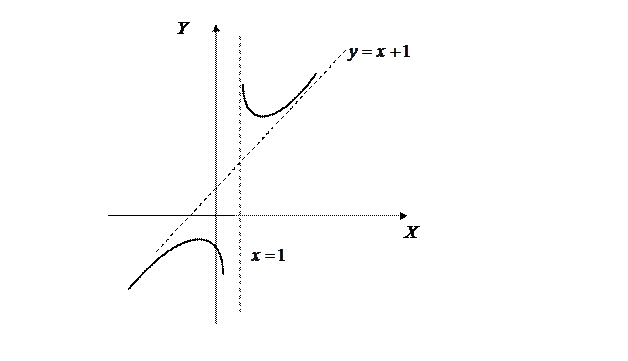
Рис.1 Построение графика функции  .
.

Задание №9. Найти неопределенные интегралы.
Пример. Найти неопределенные интегралы.
а) 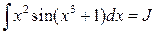 .
.
Применим подстановку  . Тогда
. Тогда 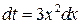 , откуда
, откуда  .
.
Таким образом, 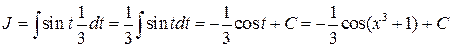
б) 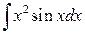 .
.
Применим формулу интегрирования по частям 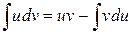 . Пусть
. Пусть
 ,
,  , тогда
, тогда 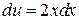 ,
, 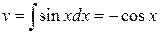 .
.
Тогда
 .
.
К интегралу в правой части снова применяем формулу интегрирования по частям. Пусть
 ,
,  ,
, 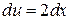 ,
, 
Таким образом,
 .
.
в) 
Подынтегральная функция является правильной рациональной дробью, знаменатель которой
 .
.
Подынтегральную функцию разложим на дроби
 ,
,
откуда
 .
.
Раскроем скобки в правой части и приведем подобные:
 .
.
Приравнивая соответствующие коэффициенты при 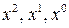 в левой и правой частях последнего равенства получим систему трех уравнений:
в левой и правой частях последнего равенства получим систему трех уравнений:

Таким образом,
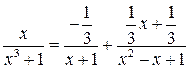 ,
,
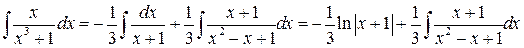 .
.
Вычислим отдельно интеграл 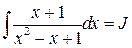 . Используя равенства
. Используя равенства
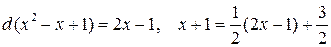 ,
,
получаем

 .
.
Отсюда окончательно вычисляем интеграл
 .
.
г)  .
.
Наименьшее общее кратное показателей корней равно 6, поэтому выполним подстановку  ,
,  , тогда
, тогда

 .
.