Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Блочное моделирование стыковка моделей.
|
|
В общем случае, независимо от структуры математического описания, стремятся строить сложную модель из элементарных моделей, применяя заранее составленные программные блоки (модули), допускающие их использование в различных моделях. Это способствует экономии средств и времени, затрачиваемых на разработку модели.
Какие блоки следует использовать в качестве программных модулей?
1. Когда речь идет о моделировании технологического процесса, такими блоками могут быть отдельные уравнения или системы уравнений, являющиеся моделями элементарных процессов.
2. В случае моделирования производственной системы программными модулями служат модели производственных участков, которые могут включать такие стандартные блоки, как датчики:
· детерминированных функций;
· случайных величин, распределенных по различным законам;
· вычисления средних значений, дисперсий и других характеристик распределений.
При блочном моделировании возникает задача стыковки элементарных моделей. Проблема стыковки моделей включает в себя несколько аспектов:
1. Первый аспект связан с вопросами вычислительного характера [15, с. 29 - 35]. Рассмотрим случай, когда элементарными моделями являются алгебраические уравнения. Оказывается, что не безразлично, относительно какой переменной разрешается уравнение. Пусть дана следующая система уравнений:
4х + у = 33, (6.1)
х + 3у = 22.
Будем решать ее методом последовательных приближений. Для этого построим итерационный контур счета, изображенный на рисунке.
   
|
Рис. 6.1- Пример правильного построения итерационного контура счета
В соответствии с этой схемой будем проводить вычисления. Выберем какое-нибудь значение для у (например, у = 29), подставим его в первое уравнение и найдем, что х = 1. Это значение х подставим во второе уравнение и установим, что у = 7. Новое значение у подставим в первое уравнение и найдем из него x и т. д. Уже на четвертом шаге мы получили решение системы х = 7, 0 и у == 5, 0. Это оказалось возможным благодаря правильному построению итерационного контура, что обеспечило устойчивость решения.
Если бы итерационный контур был построен таким образом, как на рис. 6.2, то мы не получили бы устойчивого решения. Зададим, х = 6 и из первого уравнения найдем, что у = 9. Подставим это значение у во второе уравнение и установим, что х = - 5. Снова обратимся к первому уравнению и т. д. Вычисления, показывают, что мы не приближаемся к решению, а удаляемся от него. Такое явление называют расходимостью решения. При счете на ЭВМ оно приводит к аварийной остановке.
    
|
Рис. 6.2- Пример неправильного построения итерационного контура счета
Чтобы избежать расходимости решения, нужно было уравнения решать относительно переменных, которые входят в них с наибольшими коэффициентами (первое - относительно х и второе - относительно у). В общем случае известны математические критерии, позволяющие скомпоновать систему линейных или нелинейных алгебраических или дифференциальных уравнений так, чтобы обеспечить получение устойчивого решения.
2. Вторым аспектом проблемы стыковки моделей является конструктивный аспект. Стыковка блоков должна быть конструктивно оформлена таким образом, чтобы модель могла функционировать.
Модель на рис.6.2. неработоспособна - для того, чтобы первый блок мог функционировать, нужно знать у, а для того, чтобы второй блок функционировал, должно быть известно х. Выход из ситуации - в модели должен быть какой-то блок, который введет в первое уравнение начальное значение у.
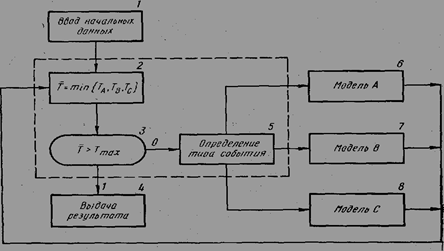
Рис.6.3
Обязательным элементом модели должен являться специальный блок, который управлял бы ее функционированием. Основная задача блока состоит в согласовании функций отдельных блоков модели. В примере для такого согласования оказалось достаточным введение начальных условий в первый блок. В общем случае управляющий блок представляет механизм, который осуществляет развитие процесса в модели согласно упорядоченной последовательности вычислений и логических операций [27, с. 193—196]. Он согласует все операции, происходящие в модели. Каждой операции в модели соответствует единственный логический путь функционирования блоков. По окончании операции управление моделью снова передается управляющему блоку, так продолжается до окончания процесса моделирования. Часто роль управляющего блока может играть датчик событий- алгоритм генерирования событий, которые происходят случайным или заранее определенным образом.
Рассмотрим модель трех производственных участков A, В и С (рис. 6.3). Функционирование модели начинается с ввода данных (блок 1). Затем из ячеек памяти машины, в которых хранятся сведения об ожидаемых событиях на участках А, В и С выбирают три ближайших события ТА, ТВ и ТС и из них устанавливается самое раннее Т (блок 2). Индексы A, В и С означают, что событие происходит на соответствующем участке. Блок 2 передает управление блоку 3.
В блоке 3 проверяется условие Т > Тмах, где Тмах - момент окончания моделирования. Если Т > Тмах, то это означает, что процесс моделирования закончился. Тогда информация о функционировании системы выводится на печать (блок 4). Если моделирование продолжается, то в блоке 5 определяется тип события и в зависимости от этого начинает функционировать одна из моделей A, В или С (блоки 6, 7 и 8). После окончания ее функционирования в памяти ЭВМ обновляется информация о ближайших событиях на соответствующем участке, и управление снова передается блоку 2. Объединение блоков 2, 3 и 5 представляет собой блок управления моделью.
3. Третий аспект стыковки- при моделировании сложных систем иногда невозможно разместить объединенную модель в ЭВМ. Тогда процесс моделирования осуществляют по частям, прибегая к так называемой статической стыковке моделей или стыковке через статистику.
Эти случаи относились к динамической стыковке. При такой стыковке блоки модели функционируют как единое целое- как в реальной системе. Выходные параметры одних блоков без предварительной обработки подаются на вход других. При статической стыковке информация о работе каждого блока не только собирается в некотором накопителе, но и статистически обрабатывается там. Существо обработки сводится к построению различных условных распределений. В этом случае внешняя информация, необходимая для функционирования какого-либо блока, поступает из накопителя в результате процедуры разыгрывания значений соответствующей случайной величины.
Пример. Пусть речь идет о прогнозировании длительности периода прогрева мартеновской плавки на модели, объединенной путем динамической стыковки моделей участков «миксерное отделение», впечной пролет» и «разливочный пролет». Этот прогноз осуществляется следующим образом.
Вначале прогнозируется длительность прогрева 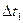 из технологических соображений. Затем с помощью модели «миксерное отделение» выясняется интервал времени
из технологических соображений. Затем с помощью модели «миксерное отделение» выясняется интервал времени  от начала прогрева до момента подачи чугуна на печь. С помощью моделей печного и разливочного пролетов прогнозируются длительности прогрева
от начала прогрева до момента подачи чугуна на печь. С помощью моделей печного и разливочного пролетов прогнозируются длительности прогрева  и
и 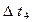 , исходя из условий организации производства на этих участках (возможные ремонты печи, задержки с подачей шлаковых чаш и др.). На основании этой информации длительность прогрева
, исходя из условий организации производства на этих участках (возможные ремонты печи, задержки с подачей шлаковых чаш и др.). На основании этой информации длительность прогрева 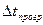 определяется как
определяется как
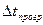 = max {
= max { 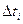 }, где I = 1, 2, 3, 4. (6.2)
}, где I = 1, 2, 3, 4. (6.2)
При статической стыковке вначале функционируют модели «миксерное отделение» и «разливочный пролет». Входная информация в эти модели задается путем разыгрывания информации о соответствующих требованиях печного пролета. С помощью моделей формируются распределения длительностей задержек периода прогрева вследствие необеспеченности плавки чугуном, шлаковыми чашами и другим оборудованием. Прогноз длительности прогрева осуществляется так же, как и при динамической стыковке моделей, с той лишь разницей, что величины  и
и 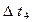 получают в результате разыгрывания предварительно найденных распределений задержек.
получают в результате разыгрывания предварительно найденных распределений задержек.
Очевидно, лучшим видом стыковки является динамическая, однако при больших размерах модели статическая стыковка может оказаться полезной, так как позволяет отдельно моделировать работу каждого блока. В силу свойств метода Монте-Карло стыковка через статистику может оказаться приемлемой для решения локальных задач (например, для проверки эффективности алгоритма управления каким-либо участком).