
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Квазистационарные токи
|
|
При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися со временем. До сих пор мы рассматривали законы постоянного тока (глава 4). Однако они оказываются справедливыми и для изменяющихся (переменных) токов, если только изменение силы тока происходит не слишком быстро. Если изменения тока настолько медленны, что за время установления электрического равновесия в цепи относительные изменения токов и ЭДС малы, то мгновенные значения токов и ЭДС будут подчиняться всем законам постоянного тока. Такие токи называют медленно меняющимися или квазистационарными. Для квазистационарного тока мгновенные значения тока оказывается практически одинаковыми на всех участках цепи.
Отметим, что скорость установления электрического равновесия весьма велика, и поэтому под понятие квазистационарных токов подпадают в обычном смысле весьма быстрые процессы. Все технические переменные токи являются квазистационарными. Даже очень быстрые электрические колебания, употребляемые в радиотехнике, с частотами порядка миллиона колебаний в секунду, очень часто можно рассматривать как квазистационарные.
Из сказанного следует, что задачи на квазистационарные электрические процессы можно решать при помощи законов постоянных токов, если применять эти законы к мгновенным значениям электрических величин. Однако при этом вместо алгебраических соотношений мы приходим к дифференциальным уравнениям, интегрирование которых и дает зависимость искомых величин от времени.
Чтобы процесс был квазистационарным, необходимо выполнение двух условий. Первое условие относится к процессам внутри проводника. Если в проводящей среде возник избыточный объемный заряд с плотностью r, то этот заряд под действием вызванного им самим поля будет уменьшаться с течением времени по закону:
r = r0× exp(-t/tМ). (44.1)
В (44.1) r0 – объемная плотность заряда в момент времени t = 0, а
tМ = ee0/s, (44.2)
где e - диэлектрическая проницаемость среды, s - ее удельная электропроводность.
Время tМ называется временем релаксации Максвелла. Оно равно времени, в течение которого объемный заряд уменьшается в е = 2, 72 раза. Следовательно, время релаксации Максвелла, определяет порядок величины времени, в течение которого восстанавливается стационарность электрических процессов. Чтобы токи можно было считать квазистационарными, характерное время рассматриваемого неустановившегося процесса Т должно удовлетворять условию:
tМ < < Т. (44.3)
Если токи изменяются периодически (электрические колебания), то под Т следует понимать период колебаний и сформулированное условие квазистационарности примет вид:
ntМ < < 1, (44.4)
где n = 1/Т – частота колебаний.
Для изоляторов время релаксации Максвелла tМ ~ минуты, для металлов tМ ~ 10-17 с.
Второе условие накладывается на размеры контура l. Дело в том, что при любом изменении электрического состояния в какой-либо части контура электрические возмущения распространяются вдоль контура с конечной скоростью, равной (глава 8):
v = c / 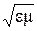 .
.
Здесь c» 3× 108 м/с скорость света в вакууме, а e и m - диэлектрическая и магнитная проницаемости среды, окружающей проводники. Если l – длина контура, то время прохождения электромагнитного возмущения вдоль контура равно
t = l/ v = (l/ c) 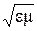 . (44.5)
. (44.5)
Для периодически изменяющихся токов условие квазистационарности будет выполнено, если
t < < Т, или ntМ < < 1, (44.6)
где Т – период изменений тока, n = 1/Т – частота колебаний.
В металлах v ~ c, и при размерах контура l =3 м, время t ~ 10-8 с. Поэтому для этого контура токи можно считать квазистационарными вплоть до частот 106 Гц (это соответствует периоду Т = 10-6 с).
В зависимости от свойств проводников одно из условий квазистационарности обычно гораздо сильнее другого, и поэтому лишь одно из них является определяющим. При изучении этой главы токи будем считать квазистационарными. Это позволит нам использовать формулы, полученные в статических полях. В частности, закон Ома для мгновенных значений квазистационарных токов.